Session Outcome Distributions for 5x Card Craps
I wanted to know what kind of variance to expect during my card craps sessions playing 5x Don’t Pass odds with a 3 roll window. So I calculated the cumulative distributions for a few strategies, based on a 100 bet bankroll (e.g., $500 @ $5 min Don’t Pass bet), a +100 bet goal (quit if double up), and a 200 game session limit (might take hours). I used simulations to find the probability density function for a single game (hand) of craps, then convolved it the number of session hands (given bankroll and goal) to get the final session distribution. Finally, I plotted the cumulative distribution function, since it’s easier to read for gambling purposes.
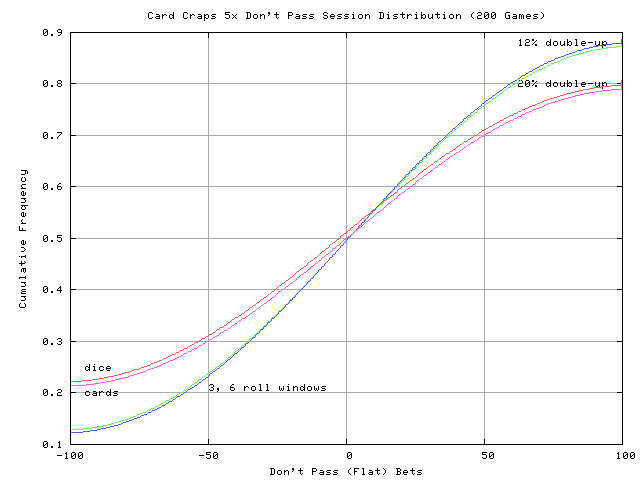
First, I compared regular dice to card craps, both laying 5x DP odds every roll. As the two curves show, they’re very similar, although the card craps game (magenta, -0.1%) returns better than normal dice (red, -1.36%). In both cases, you have more than a 20% chance of busting out (e.g., -$500 @ $5 pass line bet) or doubling up. (If you closely compare the dice and card curves, you’ll see the cards have almost an equal chance of busting out or doubling up, while the dice show a bias towards busting out.)
Next, I found that card craps performs equally well laying 5x odds with a 3-roll window or a 6-roll window. This is a nice find, since it’s pretty easy to implement the 3-roll windowed count, but practically impossible to count with a 6-roll window. [If you look closely, the 6-roll window (green) performs a little better than the 3-roll window (blue)]. The session distribution function shows about a 12% chance of busting out or doubling up. If you see where the cumulative distributions cross 50%, you’ll see that the card craps games are slightly +EV, and the dice game is of course -EV.
Not surprisingly, playing 5x DP odds with card craps has less variance than actual dice. This results mostly from the lower average bet (4.56 units/roll) for a 3-roll window, compared to dice (6.37 units/roll).
Having calculated this cumulative distribution function, I’ll probably play 5x DP with a 3-roll count, and grind out the player reward points. That’s probably the best reason to play, because you’ll easily make the Elite membership level, with it’s $20/day Free Play award. You’ll also probably make more in reward points (1 point = 1 cent) at the game than in +EV (maybe $0.005/roll). Of course, there’s always the satisfaction of beating the house, whatever that’s worth to you.
Simplified Card Craps Counting
Lately, I’ve been drawn back to the card craps (PlayCraps™) game at my local Viejas Casino, mostly because I’m willing to lay more odds now with my newfound bankroll. They’ve changed the constant shuffle machine (CSM) to the ShuffleMaster® 126 model, which has a lot more internal slots than the previous shuffler. I thought this might hurt the don’t pass advantage, but I updated my simulator parameters (now 40 slots, and 312 cards) and the results remained as good as before. Most importantly, I added a MIN_RESERVOIR_DEPTH parameter, which is the minimum number of cards in the chute (reservoir) before the CSM drops another slot. I set it to 5 cards, and experimented with various counting window depths, and max odds to find a strategy I was comfortable with.
I found that a window size between 3 and 6 rolls prior rolls didn’t make much of a difference. This was a nice result, because it’s practically impossible to remember more than two prior rolls, and the management won’t let me record rolls with paper and pen anymore 😦 I also found that laying 5x odds is enough to gain about +0.25% over the house. (10x odds yields an 1.8% edge.) Again, this is nice, because 5x is the limit of my comfort zone. So, I’ll bet $5 on the Don’t Pass line, and use a 3-roll window to determine when to lay 5x odds.
| Point | Roll Values | Lay Conditions | Notes |
|---|---|---|---|
| 4 | +4 if both die <= 3 (“low”) -4 if both die >= 4 (“high”) 0 otherwise (“neutral”) |
count >= 0 in last 3 rolls |
Lay when #(low rolls) >= #(high rolls) in window. |
| 5 | -4 if both die 5 or 6 (“ugly”) -1 if one die 5 or 6 (“bad”) +2 otherwise (“good”) |
count > 0 in last 3 rolls |
Lay if two of last three rolls are “good”. (Two “good” + one “ugly” = no edge.) |
| 6 | -5 if boxcars (“ugly”) -2 if one die 6 (“bad”) +1 otherwise (“good”) |
count >= 0 in last 3 rolls |
Lay if at most one “bad” roll in last 3. (At most one six-spot in last 3 rolls.) |
8 | -5 if snake-eyes (“ugly”) -2 if one Ace (“bad”) +1 otherwise (“good”) |
count >= 0 in last 3 rolls |
Lay if at most one “bad” roll in last 3. (At most one Ace in last 3 rolls.) |
| 9 | -4 if both die 1 or 2 (“ugly”) -1 if one die 1 or 2 (“bad”) +2 otherwise (“good”) |
count > 0 in last 3 rolls |
Lay if two of last three rolls are “good”. (Two “good” + one “ugly” = no edge.) |
| 10 | +4 if both die >= 4 (“high”) -4 if both die <= 3 (“low”) 0 otherwise (“neutral”) |
count >= 0 in last 3 rolls |
Lay when #(high rolls) >= #(low rolls) in window. |
Note that a simple counting scheme emerges from the roll types (“good”, “bad”, “ugly”) and the small window. The 4/10 are very easy to play (i.e., know when to lay DP odds). A neutral count for the 4/10 still yield a +0.15% DP odds edge. If the count gets to +12 (e.g., all three rolls “low”), the DP odds edge averages about +0.5%.
The 5/9 points also work out easily. You need 2 out of the last 3 rolls to be “good”. If there’s one “ugly” roll (-4) and two “good” rolls (+2) in the window, you’re DP odds are neutral. The 5/9 points are “fair” in that a neutral count yields no bias against the point. If all three rolls in the window are “good”, then your +6 count yields about a +0.2% DP odds edge. If you have two “good” rolls (+2), and one “bad” roll (-1) in the window, the +3 count yields about a +0.1% DP odds edge.
Finally, the 6/8 points are very easy to play as well. If two of the last three rolls are “good” (+1) and one is “bad” (-2), the neutral count still yields a DP odds edge of +0.1%. If all three rolls are “good”, the +3 count yields a DP odds edge +0.2%.
You don’t have to worry about being perfectly exact on all your counts. Usually, when I play, I pay attention to how the previous hand ended. That way, I know the roll before the come-out. The important thing is to have an adequate bankroll, and the will to lay against all points when the count is good. You’ll find that things average out well, and a game is enjoyable with enough bankroll and a +0.25% (@ 5x) tailwind.
leave a comment