Counting The Royal Match Sidebet @ Barona Casino
 My local Barona Casino offers the Royal Match blackjack side bet which pays 75-to-1 when you’re dealt a suited K-Q on your first two cards, and 2-1 for any other suited hand. Normally, the house edge is 4.06% for this side bet, but as readers of this blog know by now, sucker bets are often countable. Using a simple true K-Q count, the bet yields an average 5.4% player edge.
My local Barona Casino offers the Royal Match blackjack side bet which pays 75-to-1 when you’re dealt a suited K-Q on your first two cards, and 2-1 for any other suited hand. Normally, the house edge is 4.06% for this side bet, but as readers of this blog know by now, sucker bets are often countable. Using a simple true K-Q count, the bet yields an average 5.4% player edge.
I always play this bet for $1, and get really excited when I hit it for $75. The last time I hit it, I decided to analyze it’s countability.
I first looked at the bet’s distributions of EVs at the last hand of the shoe. This would show me if there was any potential for a counting scheme. I’d see how often and how strongly the bet went +EV. Here’s what it looks like with one deck remaining:

I could tell from the graph that the bet was exploitable. So I calculated the average profit per shoe, assuming heads-up play with the dealer. This theoretical limit comes out to a profit of +0.504 bets/shoe. That’s a really good profit rate (compare to the Dragon-7 profit rate of 0.54 bets/shoe). That means a player betting a fixed amount on the Royal Match will net an average profit equal to half his bet per shoe, when heads up with the dealer. On a per bet basis, the average Royal Match bet EV is +5.9%, assuming perfect knowledge of the dealt cards.
I then looked for a simple (practical) counting scheme that would capture most of the theoretical edge. As it worked out, the second idea that came to mind happened to be very effective. A simple true count of excess Kings and Queens yields about +0.43/shoe (85% of the theoretical edge):
trueCount = (8*decksDealt - countedKingsAndQueens)/decksRemaining
where decksDealt and decksRemaining are floating-point numbers.
The relationship between the true KQ-count and the Royal Match side bet EV is shown in the following graph:
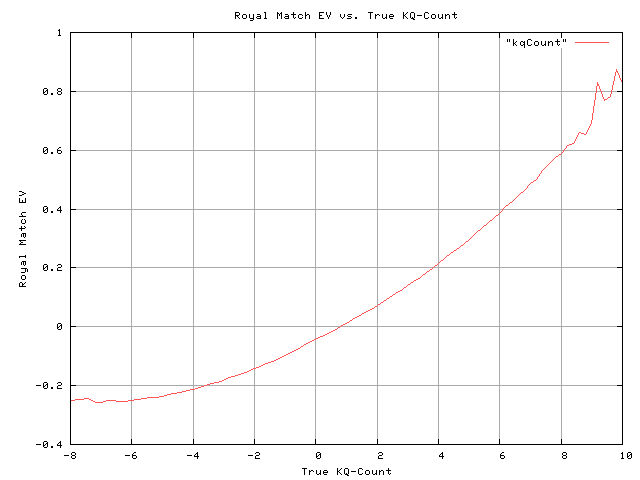
Note that you should bet the Royal Match when the true count is >= 0.8.
In heads-up play, you’ll get an average of 8.0 bets/shoe, with an average bet EV of +5.4%. The scheme is very comparable with the highly profitable Dragon-7 counting scheme (EV +0.54/shoe), but it’s much faster, and has much lower variance.
So if you don’t find me at the full-exposure Mississippi Stud game, look for me in the i-Table pit counting the Royal Match.
Instant-18 Blackjack Side Bet Counting
I recently saw the Instant-18 blackjack side bet, and I thought it was funny. It’s an even-money side bet that plays against the dealer as a hand of value 18. Hence, the name “Instant-18”. You put up a bet, and it’s an 18. It has a 2.036% house edge for a 6-deck shoe, but it’s still kind of interesting. It’s an optional side bet where (typically) you can bet an amount less than or equal to your main blackjack bet. Of course, I had to see if this bet was countable.
First, I looked at the distribution of EVs after 5 of 6 decks were dealt from the shoe:

This looked promising, so I checked out the EORs for the bet:
| Card | ΔEV |
|---|---|
| Deuce | -0.001031 |
| Trey | -0.000634 |
| Four | -0.000252 |
| Five | +0.000038 |
| Six | -0.000371 |
| Seven | -0.001946 |
| Eight | -0.000649 |
| Nine | +0.000606 |
| Ten/Face | +0.000347 |
| Ace | +0.002849 |
From the EORs, I made a simple count system, where Aces are +3, Sevens are -2, and Deuces are -1. Then I plotted the EVs of the main and side bet vs. the true count:
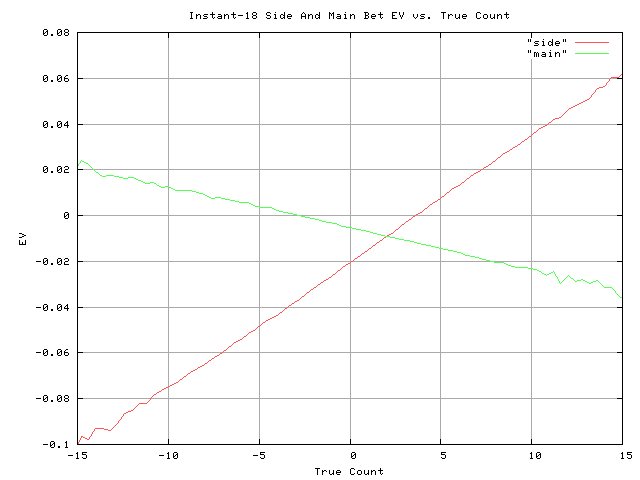
Unfortunately, when the count for the side bet gets good (true count >= 4), the main bet is -EV. However, for a good enough count (true count >= 7), the combination of (main bet + side bet) is +EV. Also, for a bad enough count (true count <= -3), them main bet is +EV.
So, by itself, the Instant-18 side bet gets good (true count >= 4) about 7.8% of the time, with an average return of +1.53%.
Of course, you can’t just bet the side bet when it gets good. You have to have a main bet to bet the side bet. If you bet both when the combination gets good (true count >= 7), or just the main bet for true count <= -3, and Wong all others, you'll bet 13.9% of the time with an average EV of +0.47%.
As usual, these things are interesting, but not practical.
Blackjack Bad Beat Progressive @ Barona Casino
My local Barona Casino offers a $1 progressive blackjack side bet that pays when your 20 loses to a dealer 21. The payout depends on the number of dealer cards, where the payout increases with the number of cards in the dealer’s hand. The progressive pays out when your 20 is beaten by a 7-or-more card dealer 21.
| Number of Dealer Cards | Payout | Probability* | Return |
|---|---|---|---|
| 7 or more cards | 100% | 4.6827e-6 | jackpot/213,500 |
| 6 cards | 1000-for-1 | 5.7405e-5 | 0.057347 |
| 5 cards | 100-for-1 | 5.0457e-4 | 0.049952 |
| 4 cards | 50-for-1 | 0.002790 | 0.136727 |
| 3 cards | 25-for-1 | 0.008282 | 0.198762 |
| 2 cards | 10-for-1 | 0.004975 | 0.044771 |
| magic card** | 20-for-1 | ~(1/26)(2/52) | ~0.028 |
| miss | -1 | ~98% | |
| total | 100% | ~0.52 + jackpot/213,500 |
*calculated using basic strategy (includes surrenders and other decisions that are not optimal for the sidebet).
**magic card average frequency assumed at 1-every-26 hands, and average 3 cards/hand
So, the break-even point for the jackpot is about $100,000. I used basic simple strategy and a 6 deck shoe in this analysis.
Effect of Shoe Depth on EV
While looking for a counting edge on this side bet, I ran into a very pronounced effect of shoe depth on the bet EV. I was expecting the random distribution of cards at the end of the shoe to distribute the EVs around 0. Well, I did find a roughly bell-shaped distribution of EVs, but I discovered that the average return decreases sharply with the shoe depth.
What this means is that as you reach the end of the shoe, the average return of the bad beat side bet decreases very quickly. Most bets don’t behave like this. You want the bet to have the same average return at the start of the shoe as at the end of the shoe. Imagine if blackjack started at a 0.5% house edge for the first hand, but for the last hand ended up at a 50% house edge, on average. Most people wouldn’t stand for that (if they knew it was happening). [You’d probably sense such a bias on an “even-money” bet, but not for a bet that hits < 2% of the time.]
I've plotted out some curves to shoe the effect of shoe depth on the bad beat EV. I set the jackpot at $100k, so the EV for a full six-deck shoe is near 0 (magic card not included). Then, I plotted EV vs. number of decks in the shoe, assuming no missing cards (i.e., a neutral shoe). So, in the graph below, 0.5 decks means half a deck.
The above graph shows the big disparity between playing the bonus at a 6-deck shoe game vs. a double-deck pitch game. The graph also reflects the bet’s average as a function of decks remaining in the shoe. Taking an extreme example (1/2 deck remaining in shoe; most houses shuffle before this point), the distribution of actual EVs is sampled in the below graph. Note how it’s shaped mostly below the -41.5% average return of the above graph.
This effect is probably due to the fact that you need a lot of perfect cards to make a 7-or-more card dealer 21. When you run low on cards, there’s probably much fewer ways (percentage-wise) to make the perfect hand. Some players might intuitively suspect this, or at least would not be surprised when they see these results.
So be careful with this bet. It gets a lot worse than you think it might, especially at the end of the shoe.
Bet The Set @ Barona i-Table
 Another bonus side bet offered on the i-Table at Barona is a version of Bet The Set that pays for various types of pairs made on the player’s first two cards. For an n-deck shoe, the probability of being dealt a pair is 13*C(n*4,2)/C(n*52,2), and the probability of a suited pair is 4*13*C(n,2)/C(n*52,2).
Another bonus side bet offered on the i-Table at Barona is a version of Bet The Set that pays for various types of pairs made on the player’s first two cards. For an n-deck shoe, the probability of being dealt a pair is 13*C(n*4,2)/C(n*52,2), and the probability of a suited pair is 4*13*C(n,2)/C(n*52,2).
| Hand | Frequency | Payout | Return |
|---|---|---|---|
| Suited Pair | 1.6077% | 20:1 | +.321543 |
| Offsuit Pair | 5.7878% | 10:1 | +.578778 |
| nothing | 92.6045% | -1:1 | -.926045 |
| Total | -.025724 |
The pit boss told me they increased the suited payout yesterday from 15:1 to 20:1, which would be an improvement of 8%, changing it from a sucker bet to a fun bet. They’re probably trying to promote the new i-Table games, and it’s an easy thing to change the payouts, since they’re not printed on the mat, but instead displayed on the player touch screens. At only a 2.5% house edge, this is very cheap as bonus bets go.
Royal Match @ Barona i-Table
 One of the nice features of the Shuffle Master i-Table is that they can change the odds of the bonus side-bets at any time. Yesterday, they increased the payout on the Royal from 50:1 to 75:1. The change showed up on the display, so I calculated the improvement.
One of the nice features of the Shuffle Master i-Table is that they can change the odds of the bonus side-bets at any time. Yesterday, they increased the payout on the Royal from 50:1 to 75:1. The change showed up on the display, so I calculated the improvement.
For an n-deck shoe, the probability of hitting a Royal (KQs) is (4)(n^2)/C(52*n,2) and the probability of getting dealt suited cards is 4*C(n*13,2)/C(n*52,2).
| Hand | Frequency | Payout | Return |
|---|---|---|---|
| Royal Match (KQs) | 0.29680935% | 75:1 | +0.222607 |
| Suited | 24.462033% | 2:1 | +0.489241 |
| nothing | 75.241158% | -1:1 | -0.752412 |
| Total | 100% | -0.040564 |
The change from the 50:1 to the 75:1 payout on the Royal improved the return from -10.2% to -4.1%. So, it went from a sucker bet to a fun $1 bet you can place every hand.
Perfect Charlie @ Fort McDowell, AZ
There’s a blackjack bonus sidebet at Fort McDowell Casino near Phoenix, AZ that offers huge payouts for a $.25 bet (you can only bet a quarter). I remember seeing this strange bet a while back, and was always curious about it. I called across state lines to find out the details, and got out the paper and pencil to calculate the house edge for a six-deck shoe.
It’s called “Perfect Charlie”, and pays jackpots for 5-card 21’s (2-3-4-5-7), with different payouts for suited and/or ordered hands. The bet also pays off hands that start off as Perfect Charlies, but don’t make it (like 2-3-4, 2-3-4-5, etc.).
I wrote up an OpenOffice spreadsheet to calculate the odds. I wanted to include the spreadsheet source in this post, but WordPress.com won’t let me upload the .ods document 😦 Fortunately, OpenOffice exports spreadsheets to html.
This is a pretty obscure sidebet, which is probably only found at Fort McDowell. Nothing popped up immediately on Google for this, so I’m having a millionth-monkey moment here (i.e., when you realise you’re the millionth-monkey pounding at the keyboard, and all-of-a-sudden Shakespeare is on the screen).
The bet is pretty horrible in terms of house edge, but want do you want for a quarter? Or actually, ($.25)(1-.6478) = 8.8¢. You get the chance to win up to $70,000, while the house has an equally small chance of getting rich off this sidebet.
| Fort McDowell Blackjack Bonus | |||||
| Bet | Hand | Conditions | Payout | Probability | Return |
| $0.25 | 2,3,4 | offsuit, any order | $10.00 | 1.98E-03 | 8.11% |
| $0.25 | 2,3,4 | offsuit, in order | $37.50 | 3.96E-04 | 5.98% |
| $0.25 | 2,3,4 | suited, any order | $75.00 | 1.41E-04 | 4.24% |
| $0.25 | 2,3,4 | suited, in order | $500.00 | 2.82E-05 | 5.64% |
| $0.25 | 2,3,4,5 | offsuit, any order | $25.00 | 7.44E-04 | 7.52% |
| $0.25 | 2,3,4,5 | offsuit, in order | $250.00 | 3.24E-05 | 3.24% |
| $0.25 | 2,3,4,5 | suited, any order | $1,000.00 | 1.26E-05 | 5.03% |
| $0.25 | 2,3,4,5 | suited, in order | $10,000.00 | 5.47E-07 | 2.19% |
| $0.25 | 2,3,4,5,7 | offsuit, any order | $50.00 | 3.30E-04 | 6.63% |
| $0.25 | 2,3,4,5,7 | offsuit, in order | $5,000.00 | 2.77E-06 | 5.54% |
| $0.25 | 2,3,4,5,7 | suited, any order | $20,000.00 | 1.29E-06 | 10.34% |
| $0.25 | 2,3,4,5,7 | suited, in order | $75,000.00 | 1.09E-08 | 0.33% |
| total | 64.78% | ||||
| decks | 6 |
Buster Blackjack @ Sycuan, CA
At my nearby Sycuan Casino, they offer a sidebet on some of their games called “Buster Blackjack”. It’s an optional “bonus” bet the player can place, up to the amount of his blackjack bet, and limited to $100. It’s a bet that the dealer will bust, and its paytable is based on the number of cards the dealer busts with.
I wrote a little recursive program to calculate the distribution of dealer busts for a 6-decks shoe, and worked in their paytable.
| Dealer Bust Cards | Payout | Probability | Return |
|---|---|---|---|
| 3 | 2:1 | 1.73032e-01 | 0.346064 |
| 4 | 2:1 | 8.93918e-02 | 0.178784 |
| 5 | 4:1 | 2.04726e-02 | 0.081890 |
| 6 | 12:1 | 2.63760e-03 | 0.031651 |
| 7 | 50:1 | 2.14444e-04 | 0.010722 |
| 8 | 250:1 | 1.15280e-05 | 0.002882 |
| no bust | -1 | 0.714240 | -0.714240 |
| total | 1.000000 | -0.062247 |
So the bet has a typical bonus bet edge of 6.2%. It’s a lot better than I thought it’d be.




7 comments