Updates to +EV Mississippi Stud @ Barona Casino
I revisited the collusion strategy for full-table (6 players), all cards exposed Mississippi Stud, as dealt at my nearby Barona Casino. I fixed a few small decision points, and calculated the EVs of the threshold points, so you can see the value of marginal calls and folds. When I play again, I’ll probably bring this chart to the table. Notice any return less than -1.0 on 3rd street is a fold (folding costs you your ante, but calling would cost more). Similarly, any return less than -2.0 on 4th street is a fold. And any return less than -3.0 on the river is a fold. For example, calling 1x on 5th street with only 2 high outs and 4 mid outs is going to cost you (-3.16)($5) = $15.80, whereas folding would limit your loss to $15. On average, this “chase” is going to cost you $0.80 more than folding. As another example, calling unsuited cards with only 2 high outs and 1 mid out on 3rd street is going to cost you (0.07)($5) = $0.35 more than folding, on average.
There are a lot of players that play way too many hands, as they don’t want to miss a payout. You can see that even the most marginal of folds is around (0.1)($5) = $0.50 for each bad decision. This can add up over each hand, and each bad decision (sometimes multiple bad decisions per hand). Often, people make multiple bad decisions per hand, making worse than -0.10 mistakes (literally, off the below chart), and betting more than $5 Antes.
| Outs | 1x EV | Notes | ||
|---|---|---|---|---|
| High | Mid | Low | ||
| 3rd Street (Offsuit) | ||||
| 3 | 0 | 0 | -0.77 | Call |
| 2 | 2 | – | -0.79 | Call |
| 2 | 1 | – | -1.07 | Fold |
| 2 | 0 | 3 | -1.05 | Fold |
| 1 | 3 | – | -0.99 | Call |
| 1 | 2 | – | -1.31 | Fold |
| 0 | 5 | – | -0.71 | Call |
| 0 | 4 | – | -1.12 | Fold |
| 0 | 3 | 3 | -0.95 | Call |
| 0 | 0 | 6 | -1.43 | Fold |
| 0 | 0 | 4 | -1.86 | Fold |
| 3rd Street (Suited) | ||||
| 2 | 0 | – | -0.87 | Call |
| 1 | 2 | 0 | -0.96 | Call |
| 0 | 4 | – | -0.75 | Call |
| 0 | 3 | 3 | -0.71 | Call |
| 0 | 3 | 2 | -0.98 | Call |
| 0 | 0 | 6 | -1.20 | Fold |
| 0 | 0 | 4 | -1.59 | Fold |
| 4th Street | ||||
| 3 | 2 | – | -1.75 | Call |
| 3 | 1 | – | -1.96 | Call |
| 3 | 0 | 5 | -1.94 | Call |
| 3 | 0 | 4 | -2.02 | Fold |
| 3 A’s | 0 | 4 | -1.86 | Call |
| 2 | 4 | – | -1.77 | Call |
| 2 | 3 | – | -1.93 | Call |
| 2 | 2 | 3 | -2.10 | Fold |
| 2 | 1 | 4 | -2.14 | Fold |
| 1 | 5 | – | -1.95 | Call |
| 1 | 4 | – | -2.13 | Fold |
| 0 | 6 | – | -1.87 | Call |
| 0 | 5 | 3 | -2.09 | Fold |
| 5th Street | ||||
| 5 | – | – | -2.68 | Call |
| 4 | 2 | – | -2.95 | Call |
| 4 | 1 | – | -3.05 | Fold |
| 4 | 0 | – | -3.16 | Fold |
| 3 | 4 | – | -2.94 | Call |
| 2 | 6 | – | -2.95 | Call |
| 2 | 5 | – | -3.05 | Fold |
| 2 | 4 | – | -3.16 | Fold |
| 1 | 8 | – | -2.95 | Call |
| 0 | 9 | – | -3.05 | Fold |
+EV Field Bet for Two Shoe Card Craps
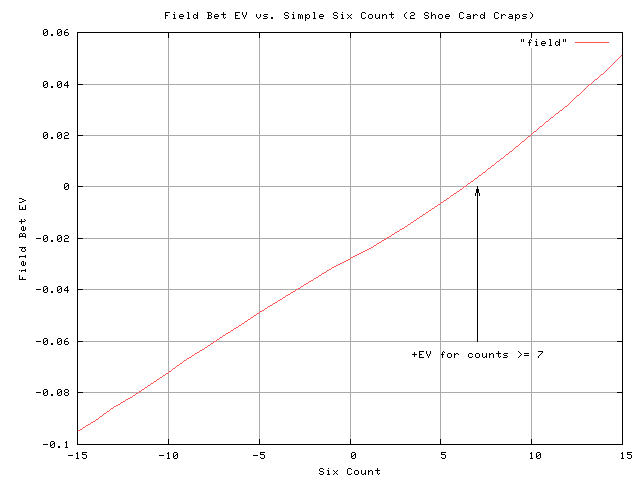
At some California casinos, craps is dealt using two 6-deck shoes, one for each die in a roll. Of course, the rolls in this type of game are not independent of each other, as a simple spreadsheet will show you. What is surprising is that a simple count of the 6-spot cards will yield +EV opportunities in the Field, provided the casino pays triple (3x) on boxcars, and double (2x) on snake-eyes on this bet. I’ve analyzed the Field bet for this game, assuming the house deals 1/2 the shoe before shuffling. The graph below shows the theoretical distribution of Field Bet expectation values (EVs) for this two shoe craps game.

The above graph shows that with exact knowledge of the cards dealt from the shoes, the Field Bet becomes advantageous (+EV) 6.44% of the time. The average advantage of a +EV Field bet using a perfect count (e.g., a spreadsheet) is 1.2%. If the house deals deeper than 50% of the shoe, these results will improve.
I found that a simple running count of the Six-spot cards is fairly good at extracting the edge out of the Field. The running Six-spot count works as follows:
- Count the number of 6-spot cards contained in every three rolls.
- Every third roll, add (1 – three_roll_six_count) to the running count.
- The Field Bet is +EV when the running count is >= 7.
Intuitively, this count make sense, because you expect to see one 6-spot card in three rolls. The running count reflects the “excess” 6-spots in the decks, i.e., how loaded the decks are with 6-spots. A simple spreadsheet shows that the sensitivity of the 6-spot card is huge on the Field, because it pays 3x for boxcars (6,6). The effect of the Aces is very small compared to the 6-spot card.
The relationship between this simple running 6-count and the Field Bet EV was verified by Monte Carlo analysis, as shown in the following results:
The simple count only yields about 60% of the opportunities found by a perfect count (the count is +EV only 3.8% of the time, compared to the theoretical 6.44% limit). So while this is an interesting find, it’d be a little boring to stand around waiting to bet the Field once every 25 rolls or so. In practice, you’d probably wouldn’t even make a bet for 2 out of 3 shoes, but you’d bet often once the shoe went +EV. Overall, the average advantage per Field bet made is a little higher than 1%, and on average you’d make a net profit of 0.058 Field bets per shoe. So, even if you’re betting $100 on the Field when it goes +EV, you’d only make $5.80 per shoe. That’s a lot of standing around for sub-minimum wage with a lot of risk. But, if you wanted to “take a shot” at making a big win with a small number of big bets, this might just be the ticket for you (especially when the count gets really good).
Rabbit Hunter ™ Stud @ Pala Casino
 I stopped by Pala Casino last weekend, and I saw a new ShuffleMaster game called Rabbit Hunter ™ Stud. It’s a really simple game, where you bet an Ante, and Tens Up Bonus bet before the hand. (The Bonus bet is technically “optional”, but since it returns 136%, you should always bet an amount here equal to the Ante.) The Tens Up Bonus bet cannot be larger than the Ante Bet. The players and the dealers each receive five cards. After looking at your hand, you may either 1) fold the hand, and lose your Ante and Tens Up bets, or 2) call the hand with a 1x Play bet equal to your Ante, or 3) call the hand with a 1x Play bet AND pay an additional 1x fee to receive one additional card (“rabbit hunt”). When you pay for the additional “rabbit hunt” card, your resulting six-hand card is used for both the Tens Up Bonus bet, and for your showdown hand against the dealer. After everyone acts, the dealer turns up his hand. The player wins the Tens Up Bonus bet for any hand greater than a pair of Tens, according to the paytable below, regardless of the dealer hand. If the dealer doesn’t qualify with Ace-high or better, the Ante bets push (no action). If the dealer qualifies, then the Ante plays for even money against the dealer hand. The Play bet always receives even money action against the dealer hand (no qualifier).
I stopped by Pala Casino last weekend, and I saw a new ShuffleMaster game called Rabbit Hunter ™ Stud. It’s a really simple game, where you bet an Ante, and Tens Up Bonus bet before the hand. (The Bonus bet is technically “optional”, but since it returns 136%, you should always bet an amount here equal to the Ante.) The Tens Up Bonus bet cannot be larger than the Ante Bet. The players and the dealers each receive five cards. After looking at your hand, you may either 1) fold the hand, and lose your Ante and Tens Up bets, or 2) call the hand with a 1x Play bet equal to your Ante, or 3) call the hand with a 1x Play bet AND pay an additional 1x fee to receive one additional card (“rabbit hunt”). When you pay for the additional “rabbit hunt” card, your resulting six-hand card is used for both the Tens Up Bonus bet, and for your showdown hand against the dealer. After everyone acts, the dealer turns up his hand. The player wins the Tens Up Bonus bet for any hand greater than a pair of Tens, according to the paytable below, regardless of the dealer hand. If the dealer doesn’t qualify with Ace-high or better, the Ante bets push (no action). If the dealer qualifies, then the Ante plays for even money against the dealer hand. The Play bet always receives even money action against the dealer hand (no qualifier).
The basic strategy for the game is very simple, according to the following rules:
- Always draw to improve your hand to any straight flush, flush, or straight (includes gutshot straight draws).
- Draw if your hand is Three-Of-A-Kind (do not draw if you already hold a full house)
- Draw if your hand is two pairs.
- Draw if your hand is a low pair (under Tens), but not if your hand is a high pair.
- Play with Ace-high or better, else fold if not drawing.
where “draw” means to pay the 1x (= Ante) amount for the extra (6th) “rabbit hunt” card.
For the following Tens Up Bonus Paytable, the house edge is only -2.25% of an Ante. That’s an especially good deal, since most games with an optional bonus bet usually cost at least 2-3% of the Ante on the main game, AND another 2-3% of the bonus bet. Here, you get to play the Tens Up Bonus Bet and the main game against the dealer hand for a combined cost of -2.25% of an Ante. Furthermore, unlike other ShuffleMaster games like Ultimate Texas Hold’Em and Crazy 4 Poker, you don’t have to make a Blind Bet (or Super Bonus Bet) that only pays a high qualifying hand. So, I’d say the cost is half that of Ultimate Texas Hold’Em, and Crazy 4 Poker (when played with the optional bonus bet).
| Hand | Return |
|---|---|
| Royal Flush | 300 |
| Straight Flush | 100 |
| Four-of-a-Kind | 50 |
| Full House | 30 |
| Flush | 10 |
| Straight | 7 |
| Three-of-a-Kind | 5 |
| Two Pairs | 2 |
| Pair Tens thru Aces | 1 |
| nothing | -1 |
Bankroll Requirements for Card Craps @ Viejas Casino
Often when I play card craps @ my local Viejas Casino, I wonder how profitable it would be to play the Don’t Pass Line, with 10x odds when the count is good. I know I could play lightning fast with a simple 3-roll window for the 5/9 and 6/8 points, and a 6-roll window for the 4/10 points. I know that this strategy would yield an average (+2.2%)(flat bet) per hand, or ($5)(2.2%) = $0.11/hand profit rate. During the week, especially during certain hours, you could be heads up with the dealer, and perhaps average 15 rolls per minute, or 3 hands per minute. So, on average, you could make about $20/hr. More importantly, you’d earn player rewards cash back at a pretty decent rate too. (I’ll take a rough guess that you’d make about $3/hr in cash back reward points.) Additionally, you’d make the MVP player level, which earns an automatic $30/day in cash back. So, if you play this game 8 hours a day, you’d average something on the order of (8hr/day)($20/hr + $3/hr) + $30/day = $214/day.
Ok, sounds great. So why don’t I do it? All I’d have to do is lay $100 against the 4 and 10 points, $75 against the 5/9, and $60 against the 6/8, unless the count is bad. I see people betting this kind of money all the time. It’s not unreasonable.
So I looked into the session outcome distributions for various bankroll, goal, and time-limit scenarios for this +EV game, to see if I could reasonably beat it.
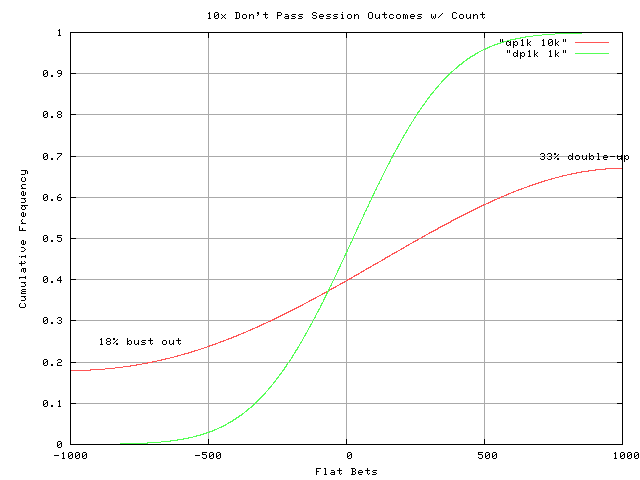
First, I looked at a bankroll of 1000 flat bets (i.e., $5000). I calculated the session outcome distributions, assuming that I quit if I busted out or doubled up (won $5000). I plotted the results as a cumulative distribution function, which is easier to read. The plot below shows the probabilities for both a 1000 hand session (6 to 8 hours), and a 10,000 hand “session” (less than a week).
What I saw immediately from the 10k hand curve (red), is that while I’d have a 33% chance of winning $5000 within a week, I’d actually have an 18% chance of busting out completely. At first, I thought that number was too high, but after I thought about it more, a 1000 flat bet bankroll is only 50 10x lays against the 4/10, or 67 lays against the 5/9, or 83 10x lays against the 6/8. So I can see how everything going wrong (which happens sometimes) could bust you out.
I included a shorter 1000 game session distribution (green) curve for people more likely to try the game for a day. You’ll average a 22 flat bet win ($110 for a $5 flat bet), and 53% of the time your outcome will be +/- 200 flat bets (+/- $1000).
I wondered if doubling the bankroll to 2000 flat bets (i.e., $10,000) would be enough to make busting out nearly impossible. I ran the analysis for a maximum of 25,000 hands, which would take between 3-4 weeks of full time play. The below graph shows that I’d still have a 7.5% chance of busting out and losing my $10,000 bankroll. That’s an improvement from the $5000 bankroll shown (green; 33% chance of busting out), but the risk of busting out is still relatively high. While I’d have a 66% chance of winning overall with the various profits listed, it doesn’t seem worth the risk to me. I don’t think it would appeal to many people. (The $1000 or so in player cash back rewards is not included in this analysis.)
The problem is that while you have a +2.2% EV/game, that percentage is only on the flat bet, and not the odds. You have to lay $100, $75, or $60 to win that $0.11/hand average.
Practical Collusion For Four Card Poker
 I continue to look at the effects of collusion on the carnival games, and today I worked on Four Card Poker. In Four Card Poker, each player is dealt five cards, from which they play their best 4 card poker hand. The dealer has the advantage of starting with 6 cards, but gives back some edge by allowing the player to raise 1-3x after seeing the hand. Also, one of the dealer cards is exposed.
I continue to look at the effects of collusion on the carnival games, and today I worked on Four Card Poker. In Four Card Poker, each player is dealt five cards, from which they play their best 4 card poker hand. The dealer has the advantage of starting with 6 cards, but gives back some edge by allowing the player to raise 1-3x after seeing the hand. Also, one of the dealer cards is exposed.
The simplest and most common strategy does not take into account the dealer upcard. The player simply calls 1x with a pair of 2’s thru 9s, and raises 3x with a pair of Ten’s or higher. This strategy yields a house advantage of 3.4%.
I worked out a very simple collusion strategy, which only requires communication of dealer upcard copies amongst the confederates. As I’ve pointed out in my posts on practical collusion for Caribbean Stud, it’s very easy to communicate how many copies of the dealer upcard the confederates hold (signal with chips, coughs, etc.). It’s very easy to know how many copies of the dealer upcard are left for the dealer to pair with. Using a simple strategy based on this upcard copies count, the house edge is cut in half down to 1.7% (on a full table).
The table below summarizes the collusion strategy when playing on a full (6 player) table. Once you know how many copies of the dealer upcard are held by the players, you play your one-pair hand according to the table. Additionally, you should 1x call AK-high when the players hold all 3 copies of the dealer upcard.
| Pair | Dealer Upcard | |
|---|---|---|
| Upcard > Pair | Upcard ≤ Pair | |
| 2’s | fold if 0-2 copies bet 1x if 3 copies |
bet 1x |
| 3’s thru 5’s | fold if 0-1 copies bet 1x if 2-3 copies |
bet 1x |
| 6’s thru 7’s | fold if 0 copies bet 1x if 1-3 copies |
bet 1x |
| 8’s | fold if 0 copies bet 1x if 1-2 copies bet 3x if 3 copies |
bet 1x |
| 9’s | fold if 0 copies bet 1x if 1-2 copies bet 3x if 3 copies |
bet 1x if 0 copies bet 3x if 1-3 copies |
| T’s thru J’s | bet 1x if 0-2 copies bet 3x if 3 copies |
bet 1x if 0 copies bet 3x if 1-3 copies |
| Q’s | bet 1x if 0-1 copies bet 3x if 2-3 copies |
bet 1x if 0 copies bet 3x if 1-3 copies |
| K’s | bet 1x if 0-1 copies bet 3x if 2-3 copies |
bet 3x |
| A’s | bet 3x | bet 3x |
Examples
You have a pair of 4’s. The dealer upcard is a 6, but nobody holds a 6 in their hands (0 copies). Fold your 4’s.
You have a pair of Jacks. The dealer upcard is a Ten, but noboby holds a Ten in their hands (0 copies). Just 1x call your Jacks.
You have a pair of Jacks. The dealer upcard is a Ten, and you and your 5 friends hold one Ten between your hands (1 copy). You should 3x raise your Jacks.
You have a pair of 8’s. The delaer upcard is a Jack, and you and your friends hold all 3 remaining Jacks (3 copies). You should 3x raise your pair of 8’s.
Simple +EV Collusion For Caribbean Stud
This is an update to my previous collusion analysis for 6 players. I found that Caribbean Stud games actually seat 7 players, and I constructed a simple collusion strategy that yields a +1.1% player advantage.
If you enjoy playing Caribbean Stud, and have a set of friends that can fill up a table, there’s a simple way to play together to obtain a +1.1% advantage against the house. Here’s what each player (i.e., you and your 6 confederates) need to do:
- For each copy of the dealer up card a teammate holds, he places a $5 chip (red) in a designated signaling area.
- For each remaining Ace or King a teammate holds, he places a $1 chip (blue) in the designated signaling area.
- Each player now knows how many total copies of the dealer upcard the confederates hold, as well as additional Aces and Kings.
- Each player adjusts the basic strategy decision according to the table below (i.e., confederates know when to Raise with junk, and fold weak hands).
| Hand | Modified Strategy |
|---|---|
| Junk | Raise if see at least 3 red chips and 4 blue chips. (3 upcard copies and 4 A/Ks.) |
| A K J 8 3 | Fold unless 3 red chips seen. (All upcard copies held by friends.) |
| One Pair 2’s thru 6’s | Fold if upcard is higher than pair, unless 2 or more red chips seen. (2 or more upcard copies.) |
| One Pair 7’s thru K’s | Fold if upcard is higher than pair, unless 1 or more red chips seen. (1 or more upcard copies.) |
While this collusion strategy is non-verbal, and no one will really care if you do it for $10 bets, the casino would very quickly catch on to a table full of $100 Ante players all calling with junk at the same time. Otherwise, a table full of players would make on average (7 players)($100/player)(1.1%/hand)(40 hands/hr) = $308/hr. And of course the variance would swamp the average for any reasonable time frame (i.e., shorter than months).
Examples
Let’s say your hand is a pair of Kings. The dealer upcard is an Ace. Your confederates do not hold any Aces (i.e., they place no red chips in their signaling areas). You should fold the hand.
Say you have junk. The dealer upcard is a Trey. Your confederates indicate they have all the Treys in their hands (they place 3 red chips in the signaling areas). The confederates also place 5 blue chips, signaling they have 5 Aces/Kings between them. Everyone should call (2x) no matter what they hold.
The dealer upcard is a King. The confederates place 3 red chips, indicating they have all the King “outs”. They also place 4 blue chips, indicating they have all 4 Aces between them. Everyone should call, no matter what they have, since there are at least 3 red chips and 4 blue chips seen.
You have a pair of Treys. The dealer upcard is a Ten. The confederates place 2 red chips, indicating they have 2 Tens between them. You should call your hand. Junk hands should fold.
Double Baccarat @ Sycuan Casino
My local Sycuan Casino offers a unique game that’s a simplification of Pai-Gow tiles. Like the tile game, the players and the bank are dealt 4 cards each. Each hand is set into a front hand of 2 cards, and a back hand of two cards. The back hand must be greater than the front hand. Hand values are ranked by poker pairs, followed by Baccarat totals (0 thru 9). After the player hands are set, the bank turns over its hand and sets it according to “House Way”.
| Hand | Rule |
|---|---|
| Two Pairs | Set large pair behind, small pair in front. (Pair-Pair; never break pair). |
| Pair Aces | Pair Aces behind (never split Aces.) |
| One Pair | Pair behind if 5 or higher front, else Split pair if can form (8,8), (7,9), (8,9) or (9,9), else Pair behind. |
| No Pair | Set (5,9) if possible, else Set hand with highest front + back total, with minimum back – front gap. |
Once all hands are set, the player or banker wins the wager if hands win/win, tie/win, or win/tie. In the case of tie/tie, the bank wins the wager. All other hands push the wager.
The player posts a minimum 1% collection before each hand. If all players push their bets, all collections are returned (“free collection”). This means in a heads-up game against the house, the player only pays the collection for a win or a loss, and gets free collection on a push.
I worked at optimizing a heads-up player strategy against the a house way bank, out of curiosity at what the house edge was. Of course, its an uphill battle against the collection (even when free for pushes), and worst, losing tie/tie. Using exhaustive combinatorics, I came up with the following near-optimal strategy (I only looked at the no-pair cases):
| Hand | Rule |
|---|---|
| Two Pairs | Set large pair behind, small pair in front. (Pair-Pair; never break pair). |
| Pair Aces | Pair Aces behind (never split Aces.) |
| One Pair | Pair behind if 5 or higher front, else Split pair if can form (8,8), (7,9), (8,9) or (9,9), else Pair behind. |
| (6,9), (7,9), (8,9), (9,9) | |
| front + back = 14 | (7,7), (6,8) |
| (5,9) | |
| front + back = 10 | (5,5) |
| (9,1) | |
| (4,6), (3,7), (2,8) | |
| front + back = 9 | (0,9) |
| (1,8) | |
| (4,5), (2,7) | |
| front + back = 8 | (0,8) |
| (1,7) | |
| (3,5), (2,6) | |
| front + back = 7 | (3,4) |
| (0,7) | |
| (2,5), (1,6) | |
| front + back = 6 | (2,4) |
| (0,6) | |
| (1,5) | |
| Set hand with highest front + back total, with minimum back – front gap. | |
This strategy simulates at -1.46% heads up against house way, when minimizing collection to 1% of the bet amount. The frequency of ties simulates at 1.12%. So even if they eliminated the bank wins tie/tie rule, you’d still lose because of collection. As an additional note, if a heads-up player also plays the same House Way as the bank, the house edge increases to 2.0%.
Overall, the head’s-up game is about as good as a free-collection Pai-Gow game. (There are a few free-collection games at the card rooms town.) However, since the casinos don’t offer free-collection Pai-Gow, the head’s-up Double Baccarat game has better odds than the Pai-Gow game, for what it’s worth.
Card Craps @ Viejas Is The Best Ever
I’ve been playing more and more card craps @ Viejas, because I’ve found a more socially acceptable and enjoyable way to take advantage of the Don’t Pass bias of the game. Counting is very easy now, since I only need to remember a few things about the last 3 rolls. Ideally, playing 10x odds with the strategy below yields about +1% player advantage of the flat bet (+EV). And whenever you’re laying/taking odds, you have a relatively large advantage on your odds.
Here’s what I do. I start out with a $5 bet on both the Pass Line and the Don’t Pass Line for every hand. Then I either take or lay odds depending on the count for the point. Yes, I know this will cost me more house edge, but there’s a few good reasons to make this additional bet. First, people always look at the “Don’t player” with a little bit of animosity, and being “against” the table takes a lot of fun out of the game. Secondly, you can easily account for how much “house edge” you’ve paid to play, by adding up all the times boxcars hit on the come out roll. Also, the occasional time you lose $5 to boxcars is a lot less aggravating than losing 4 or 5 DP bets in a row to 7-11. But most importantly, if the count gets good during the roll (esp. for the 5/9, and 6/8), you can take pass line odds and cheer with the table for the point. And, when you’re right, you get some extra non-monetary satisfaction.
3-Roll Window Strategy
I’ll review the simple counting strategy for a 3-roll window. You get very little improvement for increasing the window to 4, 5, or 6 rolls, so it’s not worth the considerable effort to try to remember anything more than a few features of the last 3 rolls.
| Point | Key Cards | When To Lay | Roll Count Values |
|---|---|---|---|
| 4 | ⚀, ⚁, ⚂ | When more “low” rolls than “high” rolls in last 3 rolls. A low roll has two key cards. A high roll has no key cards. A mixed roll is neutral. |
+4, 0, -4 |
| 5 | ⚄, ⚅ | Less than 2 key cards in last 3 rolls. | +2, -1, -4 |
| 6 | ⚅ | Less than 2 key cards in last 3 rolls. | +1, -2, -5 |
| 8 | ⚀ | Less than 2 key cards in last 3 rolls. | +1, -2, -5 |
| 9 | ⚀, ⚁ | Less than 2 key cards in last 3 rolls. | +2, -1, -4 |
| 10 | ⚃, ⚄, ⚅ | When more “high” rolls than “low” rolls in last 3 rolls. A high roll has two key cards. A low roll has no key cards. A mixed roll is neutral. |
+4, 0, -4 |
The counts for pass and don’t pass on a given point are multiplicative inverses of each other (i.e., times -1). So while `Yo is +4 for the pass line odds on the 6-point, it is -4 against the don’t pass odds for the 6-point, etc.
When the conditions aren’t good to lay odds, then they’re automatically good to take pass line odds. This is how you play. Start off with both a minimum pass line and don’t pass flat bet. As soon as the point is established, think back about the previous 3 rolls. Lay odds if the conditions are met for the point as described in the above table. Otherwise, it’s good to take odds on the pass line bet. So you’re constantly monitoring the key cards for your point, and adjusting your odds bet accordingly.
Odds Advantage Depends On Count
You can read more about the fair-weighted count values for each roll on my main page on card craps. While the above table works fine for knowing when to lay and when to take odds on a point, knowing the details of the count will tell you how good your odds are. The following graph shows the advantage you obtain on your odds (pass and dont) for a given 3-roll windowed count. (When the count is positive, lay odds; when the count is negative, take odds. You always have an advantage on your odds.)
The tables below lists the possible count values and advantage for the points shown in the above graph.
| Count | Don’t Pass Odds Advantage | Pass Line Odds Advantage |
|---|---|---|
| -12 | +2.2% | |
| -8 | +1.3% | |
| -4 | +0.43% | |
| +0 | +0.41% | |
| +4 | +1.3% | |
| +8 | +2.2% | |
| +12 | +3.1% |
| Count | Don’t Pass Odds Advantage | Pass Line Odds Advantage |
|---|---|---|
| -12 | +2.4% | |
| -9 | +1.8% | |
| -6 | +1.2% | |
| -3 | +0.59% | |
| +0 | +0.0% | |
| +3 | +0.59% | |
| +6 | +1.2% |
| Count | Don’t Pass Odds Advantage | Pass Line Odds Advantage |
|---|---|---|
| -10 | +1.5% | |
| -8 | +1.1% | |
| -7 | +1.1% | |
| -6 | +0.66% | |
| -5 | +0.65% | |
| -3 | +0.21% | |
| -2 | +0.22% | |
| +0 | +0.20% | |
| +3 | +0.65% |
In the above tables and graphs, “odds advantage” means that on average return of your odds bet for a given count, excluding no result rolls. For example, if the count is +12 against a 10 point (the last three rolls were high), then your advantage of 7-out is 3.1% of your total lay bet, compared to hitting another 10. Of course, your actual return is lower, because no result is likely in the next roll. But, you’re (2)(+3.1%) = 6.2% more likely to hit a seven vs. a 10 for a +12 count than for a neutral count.
So overall, you’ll have about a +1% player edge on your flat bet. This, of course, is very little to get excited about on its own. However, you can see that you’ll have a relatively large “advantage” for your odds bet on most rolls. So, when the count is really good, it’s really fun to lay 10x odds, or take 10x odds. For example, say the count is -8 on a 6. It’s a good time to take 10x odds on your pass line bet for the 6. Your chances of hitting the 6, weighted by the 6:5 payout, is 1.1% better than your chances of 7-out. Of course, most likely, the next roll will not be a 6 or a 7, and the count will change. But when you take or lay your odds, you have the edge.
Watching Rolls
After a little practice, it gets easy to count in a 3-roll window. A little discussion with examples will help you get the idea on how to count at the table.
When watching the come out roll, keep in mind the previous roll. Say the come out is (5,2) = 7 pass line winner. You push. Say the next roll is (5,3) = point 8. If you don’t remember snake eyes two rolls ago, then lay some odds against the 8. Now, watch the rolls, and pay attention to the Aces. One ace in the 3 roll window is okay. However, if you see two Aces in the last three rolls, move to the pass line odds. So you’re just paying attention to the aces, and where they are in the window. Aces in consecutive rolls means you’re going to bet pass line odds. If the next roll doesn’t have an Ace, it’s still good for the pass line for one roll. However, you need an Ace to remain on the pass line, otherwise switch and lay odds against. The 6 point is similar to the 8 point, except the six-spot is the key card.
The 4 and 10 points are the easiest to play. It’s really easy to see “high” and “low” rolls. Low rolls are when both dice have 3 or less spots. High rolls are when both dice have 4 or more spots. Mixed rolls are neutral. When a point comes out as 4 or 10, it’s likely that the count is good to lay against. If a 3 neutral rolls go by, then the windowed count is neutral, and still favor laying against the point by +0.4%. However, as soon as the count goes from neutral to negative (e.g., Ace-Deuce vs. 10 point), then take odds on the pass line.
The 5 and 9 points are fun to play, because they’re “fair” and not biased. Of course, the roll establishing the point is +2 against itself, so it’s likely you’ll start out laying against the point. However, the count swings + and – very quickly, and any time there are 2 or more key cards in the window, take odds on the pass line. For example, say the come out roll is (6,5) `Yo. The next roll is (2,3). You should definitely take odds on the pass line, because the count is at least +2, depending on what the roll before the `Yo was. Now, watch the next roll. No matter what, the count will still be at least +2, because of the +4 `Yo, so you always place odds for at least two rolls after a +4 roll.
Conclusion
The game is really fun for counting. It makes the game a lot more fun than watching completely random dice, and relying on pure luck. Card craps has a reasonable component of skill, because odds change significantly with every roll.
Of course, this kind of thing might not be what the typical craps player is looking for. I’ve found that almost everyone tries to play “regular craps” at the card craps table. This can be a problem, because blind pass line odds in this game gives the house a huge house advantage. (Taking 10x odds in a dice craps game makes your overall odds better, because it reduces the proportion of the house edge by the odds factor. However, in card craps, there’s an inherent don’t pass bias, where blind 10x don’t pass odds yields a +1.8% players advantage, but blind 10x pass line odds gives the house a 4% edge vs. the nominal 1.4% pass line cost.)
Simple Collusion Strategy for Caribbean Stud
 (This post was calculated for 6 players; see updated analysis for +EV collusion with 7 players.)
(This post was calculated for 6 players; see updated analysis for +EV collusion with 7 players.)
I’ve always wondered how easy and effective collusion at Caribbean Stud would be. People have looked into the theoretical gains of collusion, and conclude its possible to reduce the house edge to 0.4%, using a computer to analyze all 30 confederate cards and the dealer upcard.
I developed a practical collusion strategy for Caribbean Stud, which reduces the house edge from a practical 5.32% down to 1.32% with 6 players. That’s a significant savings, since often players are grinding away, trying to hit a large progressive, or a high hand bonus overlay. On a $5 bet, a normal strategy costs ($5)(.0532) = $0.266/hand. That’s pretty expensive, close to $11/hr @ 40 hand/hr. Using the simple collusion strategy detailed below, you’d cut your costs by 75%, down to ($5)(.0132) = $0.066/hand, or $2.64/hr. That’s a big deal, especially if you play a lot, or for long sessions. Normally, Caribbean Stud is an expensive game, long-term.
To collude, you’ll need a cooperative table of 6 players (you and 5 others). You don’t need much info, and the strategy implementation is extremely simple. The key is calling a nominal folding hand, when you have enough info to justify a call, in hopes the dealer doesn’t qualify. Also, there are times when you should fold a normal calling hand, because it’s likely that the dealer holds a better hand.
The easiest way to share the needed info among players is by signaling with colored chips. In designated per-player areas, each confederate should place a red ($5) chip to indicate each copy of the dealer upcard they posses. Additionally, each player should place a blue ($1) chip for every Ace or King they hold. With this collusion information, you should modify the simple strategy as follows:
| Hand | Modified Strategy |
|---|---|
| Junk | Raise if see at least 3 red chips and 3 blue chips. (3 upcard copies and 3 A/Ks.) |
| A K J 8 3 | Fold if one or less red chips seen. (1 or less upcard copies.) |
| One Pair 2’s or 3’s | Fold if one or less red chips seen, AND upcard is higher than pair. (1 or less upcard copies.) |
| One Pair 4’s thru 8’s | Fold if no red chips seen, AND upcard is higher than pair. (No upcard copies.) |
| Pair 9’s or higher | No change. |
Raising with Junk
The following table shows the simulated average value of raising with a junk hand, given the 6 confederates have all 3 copies of the the dealer upcard (not A/K), broken down by the number of Aces and Kings the confederates hold. For example, say the dealer upcard was a 9c, and the players have all the remaining nines (9d, 9h, 9s). Then, the table below says not to raise junk unless the confederates (i.e., 30 cards seen) hold any combination of at least 3 Aces and/or Kings. So if the confederates hold 2 Aces and 2 Kings, the value of raising a junk hand is -0.66649. This is much better than folding (value -1). Or, if the confederates hold 0 Aces and 4 Kings, the value of a junk hand is -0.67487. On the other hand, if the confederates hold only 1 Ace and 1 King, then it’s better to fold the junk hand (-1) than raise it (-1.05500).
0 Kings 1 King 2 Kings 3 Kings 4 Kings
4 Aces -0.69915 -0.55349 -0.50180 -0.51584 -0.69635
3 Aces -0.84700 -0.67379 -0.54392 -0.49117 -0.51812
2 Aces -1.05753 -0.84399 -0.66649 -0.54415 -0.48636
1 Ace -1.29684 -1.05500 -0.84116 -0.66779 -0.53230
0 Aces -1.54412 -1.29312 -1.04717 -0.85175 -0.67487
Note that the table is symmetrical about the diagonal Aces=Kings, and can be reduced using the index Aces+Kings:
| Known Aces+Kings | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| EV(Raise) | -1.54 | -1.30 | -1.05 | -0.85 | -0.67 | -0.54 | -0.50 | -0.52 | -0.70 |
The frequency of 6 confederates (30 cards) holding all 3 the dealer upcard outs is a high 19.5% = C(48,27)/C(51,30). That means in one out of five hands, a few confederates will probably be helped. Remember, that raising a junk hand with a value of -0.70 is better than folding (-1), and for a $5 Ante, that’s a $1.50 savings. Any time you can play a slow carnival game for around 2% of the Ante, you’re doing well. Caribbean Stud is a fun, relaxing game, but it’s normally expensive. Reducing its house edge from 5.5% to 1.3% makes it a lot more enjoyable.
Card Craps Source Code
The card craps players at Viejas definitely lean towards Don’t Pass now, even when I’m not at the table 🙂 The astute players understand that the game is unlike dice craps, and the rolls aren’t quite independent of each other. Yesterday a Don’t player I’ve never seen before started to lecture me on this point before I could tell him I agreed. Then a young couple came and started playing DP and laying odds, like they knew what was going on. When the regulars are playing, at least half the table plays Don’t.
Anyways, I decided to clean up and post my Java source code for card craps, including the CSM model, the roll window, etc. You can download my source code, inspect the models, experiment with the parameters, and verify my results (+1.5% of the flat bet @ 10x Dont’ Pass odds using 3-roll count for the current Viejas shuffler; -3.6% for 10x odds Pass Line player!). I’m posting the source code to show how simple the CSM effect is on the craps game. I.e., given a simple but accurate model of the CSM, the Don’t Pass edge follows:
import java.util.Vector;
import java.util.Random;
/**
*
* @author show
*/
public class CSM {
// params approximate the ShuffleMaster 126 model Constant Shuffle Machine
static final int NUM_SLOTS = 40;
static final int DICE_SETS = 52;
static final int MIN_BUFFER_DEPTH = 4; // minimum cards in chute
protected Vector[] slot = new Vector[NUM_SLOTS]; // card slots in "wheel"
protected Vector chute = new Vector(); // cards are dealt from chute
protected Random random = new Random();
public CSM() {
for (int i=0; i<NUM_SLOTS; i++) {
slot[i] = new Vector();
}
// load dice
for (int i=0; i<DICE_SETS; i++) {
for (int d=1; d<=6; d++) {
shuffleCard(d);
}
}
}
// shuffle roll back into CSM
public void shuffleRoll(Roll roll) {
shuffleCard(roll.getDie1());
shuffleCard(roll.getDie2());
}
public Roll dealRoll() {
return new Roll(dealCard(), dealCard());
}
// deal card from chute
protected int dealCard() {
// drop a slot if chute is running out of cards
while (chute.size() < MIN_BUFFER_DEPTH) {
// select a random slot of cards from the "wheel"
Vector randomSlot = slot[random.nextInt(NUM_SLOTS)];
// drop slot of cards into the chute
chute.addAll(randomSlot);
randomSlot.clear();
}
return (Integer) chute.remove(0);
}
// shuffle card into random position of random slot
protected void shuffleCard(int card) {
Vector randomSlot = slot[random.nextInt(NUM_SLOTS)];
if (randomSlot.isEmpty()) {
randomSlot.add(card);
} else {
int randomPosition = random.nextInt(randomSlot.size());
randomSlot.add(randomPosition, card);
}
}
}



leave a comment