Bet The Set @ Barona i-Table
 Another bonus side bet offered on the i-Table at Barona is a version of Bet The Set that pays for various types of pairs made on the player’s first two cards. For an n-deck shoe, the probability of being dealt a pair is 13*C(n*4,2)/C(n*52,2), and the probability of a suited pair is 4*13*C(n,2)/C(n*52,2).
Another bonus side bet offered on the i-Table at Barona is a version of Bet The Set that pays for various types of pairs made on the player’s first two cards. For an n-deck shoe, the probability of being dealt a pair is 13*C(n*4,2)/C(n*52,2), and the probability of a suited pair is 4*13*C(n,2)/C(n*52,2).
| Hand | Frequency | Payout | Return |
|---|---|---|---|
| Suited Pair | 1.6077% | 20:1 | +.321543 |
| Offsuit Pair | 5.7878% | 10:1 | +.578778 |
| nothing | 92.6045% | -1:1 | -.926045 |
| Total | -.025724 |
The pit boss told me they increased the suited payout yesterday from 15:1 to 20:1, which would be an improvement of 8%, changing it from a sucker bet to a fun bet. They’re probably trying to promote the new i-Table games, and it’s an easy thing to change the payouts, since they’re not printed on the mat, but instead displayed on the player touch screens. At only a 2.5% house edge, this is very cheap as bonus bets go.
Royal Match @ Barona i-Table
 One of the nice features of the Shuffle Master i-Table is that they can change the odds of the bonus side-bets at any time. Yesterday, they increased the payout on the Royal from 50:1 to 75:1. The change showed up on the display, so I calculated the improvement.
One of the nice features of the Shuffle Master i-Table is that they can change the odds of the bonus side-bets at any time. Yesterday, they increased the payout on the Royal from 50:1 to 75:1. The change showed up on the display, so I calculated the improvement.
For an n-deck shoe, the probability of hitting a Royal (KQs) is (4)(n^2)/C(52*n,2) and the probability of getting dealt suited cards is 4*C(n*13,2)/C(n*52,2).
| Hand | Frequency | Payout | Return |
|---|---|---|---|
| Royal Match (KQs) | 0.29680935% | 75:1 | +0.222607 |
| Suited | 24.462033% | 2:1 | +0.489241 |
| nothing | 75.241158% | -1:1 | -0.752412 |
| Total | 100% | -0.040564 |
The change from the 50:1 to the 75:1 payout on the Royal improved the return from -10.2% to -4.1%. So, it went from a sucker bet to a fun $1 bet you can place every hand.
Session Outcome Distributions for Ultimate Texas Hold’Em
The most common mistake players make in UTH is to not bet their hands, especially preflop (i.e., raising 4x according to basic strategy). Certainly, if your initial bankroll is small, like 20 Antes, it’s clear that if you quickly lose three 4x raises, then you’re out. On the other hand, you can just as easily double up for a nice hit-and-run.
I’ve calculated the probability distributions for a few session scenarios, given 1) starting bankroll, 2) hit-and-run goal, and 3) maximum number of hands (session length). These distributions are calculated using basic strategy, i.e. betting a hand whenever long-term advantageous. Hopefully, these scenarios will help you understand the possible outcomes of your sessions, and their likelihoods.
100 Ante Bankroll, Leave if Double-Up or Bust-Out, 100 Hands Max
Let’s say you sit down with a bankroll of 100 Antes (i.e. $500 for a $5 Ante game). You decide before hand that you’ll play a maximum of 100 hands (about 3 hours), and that you’ll leave if you double up (+$500 profit), or bust out. In this scenario, you have an equal chance (1.5%) of busting out or doubling up. Otherwise, 97% of the time you’ll end up somewhere in-between, following the distribution below:
20 Ante Bankroll, Leave if Double-Up or Bust-Out, 100 Hands Max
In this example, say you have only 20 Antes (i.e., $100 total bankroll for a $5 Ante game). You plan to leave if you double-up or bust out, and to play a maximum of 100 hands (~ 3 hours). In this scenario, you’ll have a 33% chance of busting out, a 27% chance of doubling up, and a 40% chance of falling somewhere in-between, following the distribution below:
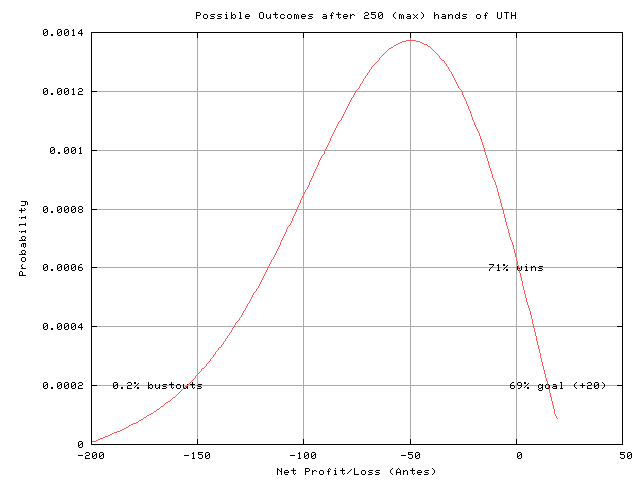
200 Ante Bankroll, Leave if Win 20 Antes or Bust-Out, 250 Hands Max
Say you have a big bankroll, are happy to hit-and-run after winning 20 Antes (i.e., $100 in a $5 Ante game), and are willing to grind out 250 hands. In this case, you have a 69% chance of making your $100, an overall 70% chance of winning, and only a 0.2% chance of busting out. The remaining 30% of the time, you’ll fall somewhere in-between, according to the following distribution:
Playing “Forever” for 0.8 Antes/hr
Personally, my only goal is to play UTH “forever” and lose (2.3% Ante/hand)(35 hands/hr) = 0.805 Antes/hr. For a $5 Ante game, that’s only a cost of $4/hr. I consider that cheap entertainment, and Casino Pauma gives back more than that in player rewards and cashback. There, your only effective costs are your dealer tokes.
Still, there’s always the risk of running bad, and busting out a limited bankroll. (And the equal chance of running good and doubling your entire bankroll, or hitting a Royal Flush, and becoming a “lifetime winner” for a while). I computed an outcome distribution over 3000 hands, starting out with a 500 Ante bankroll (i.e., $2500 for a$5 Ante game), and adding back $4/hr to your bankroll (either from cashback, or chalking it up to cheap entertainment). For this scenario, there’s still a 3.5% of busting out, and a 3.5% chance of doubling-up. Otherwise, 93% of the time, you’ll end up somewhere in-between according to the following distribution:
Conclusions
The probability density function of the outcome of a single basic strategy UTH hand was calculated, and used to compute the session outcome distribution for a scenarios of bankrolls, goals, and session times. In each scenario, the simulated 2.3% Ante/hand house edge is seen, no matter the shape of the distribution.
2nd Nut Kicker on Unpaired Board (UTH)
A lot of times when playing Ultimate Texas Hold’em, you’ll be faced with a 1x river call with a bare minimum kicker. It probably occurs to you that the strength of your call depends on how much of the board the other players have hit. For example, say you’re looking at 1x calling an unpaired board with 2nd nut kicker. Basic strategy says to call if it’s not a scare board, nor gutshot board, and there’s no possible flush on board, or if both your kickers play. (This situation occurs 1.3% of the time if you play basic strategy, and more frequently if you play less aggressively than basic strategy.) Your odds are better if the players at the table connected with the board (made a lot of pairs) than if everyone missed. I ran some simulations to quantify this effect, to show how you can use table information to improve this call.
| total players |
total pairs | notes | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| 2 | +1.3% | +11% | +17% | always call | ||
| 3 | -3.4% | +5.3% | +12% | +21% | +33% | fold if no pairs |
| 4 | -5.3% | -0.0% | +7.8% | +16% | +26% | fold if < 2 pairs |
| 5 | -16% | -5.8% | -1.4% | +11% | +21% | fold if < 3 pairs |
| 6 | -28% | -16% | -4.7% | +4.9% | +14% | fold if < 3 pairs |
So, for example, say you have Jh 2s and the board is Ah Ks Th 9d 3s. With no more information, the odds are that you should call (+19.1%). However, if you’re at a full table (6 players), and all the other players only made 2 pairs with the board, then you should fold. The percentages of the table don’t exactly apply to this specific case, but are averages over 20 million hands, and all cases where basic strategy said to call with 2nd nut kicker.
Practical Collusion for Ultimate Texas Hold’em
Most casinos that spread Ultimate Texas Hold’em don’t really mind when players discretely show their hands to their neighbors, or even flash the entire table. This is because overall, a player can’t gain much advantage by doing so. While the player will definitely pick up an edge WHEN possessing a borderline hand AND partner information indicates to alter basic strategy, these conditions don’t occur frequently enough to make much of a difference.
How To Collude
Collusion helps only on borderline cases. When you have a solid hand (e.g., 55’s, KTo, A7o, etc.) don’t bother trying to get neighbor info, just raise. If you have a marginal raising hand (J8s, JTo, Q6s, Q8o, K2s, K5o) then it helps to see your immediate neighbor’s cards, or ideally, see if two of your outs are held by the entire table. Finally, if you have a hand just below the raising threshold, or a pair less than 5’s, then you need full table information before raising.
Using Immediate Neighbors
Sometimes, it’s only practical to see the cards of your immediate neighbors, or otherwise communicate with them. This is very helpful for the marginal raising hands. The tables below show that you should only raise the marginal hands if your immediate neighbors (up to 3 of them) don’t have any of your outs. For example, if you know that among 4 hands (yours included), you have the only K and 5, then 4x raising K5o is worth +14% (of the Ante) than checking it. However, if your neighbors have a K or 5, then 4x raising is a mistake. The same pattern is seen for all the marginal raising hands.
When you only have access to immediate neighbors, then use the column of the tables below for the number of hands you have information for. It doesn’t matter what the other’s players (“dark hands” you can’t see) are holding. It just means you can only use the 4-player or 3-player columns in the tables.
Asking The Whole Table
In some cases (say you’ve filled the table with your friends), you can test the whole table for your outs. If communication with the table is good, you can ask “Should I raise K5o?”. This really means, “Does anyone have a K or 5?”. If you get just one response (meaning, “Yes I have one”), then go ahead and raise, you’re still better off by +7.5% to raise 4x than check). However, if you get two responses, then two of your outs are gone, and you should not raise, since it’s 7.5% better to check. If no one has any of your outs, then raising is worth +22% more than checking.
You can use the whole table for advanced collusion play. There are a set of hands a few notches below the minimum raising threshold that are actually good to raise when all their outs are still in the deck. These hands are listed in the table below under “Marginal Checking Hands”. For example, you would ask the table, “Should I raise K4o?”. Of course, basic strategy says to check this hand, and you’re really asking, “Does anyone have a K or 4?”. If you find no one has your outs, then it’s worth raising, by a long shot (e.g., +18% at a full table, +8.9% for 4 players).
Pocket Pairs
Basic strategy says to raise all pocket pairs except deuces. However, for 2’s thru 5’s, knowing how many outs are already gone (in the players hands) will allow you to make a better decision. The below table shows you the difference between checking and raising 4x for these pairs, given the number of players at the table, and how many of your outs are seen. Note that for 5’s or higher, you should still raise even if all your outs have been seen.
| Total Players @ Table | ||||||
|---|---|---|---|---|---|---|
| Hand | 2 | 3 | 4 | 5 | 6 | information |
| 22 | -8.1% | -5.1% | -2.0% | +0.8% | +4.7% | no outs seen |
| -40% | -39% | -37% | -34% | -32% | one out seen | |
| 33 | +12% | +15% | +18% | +20% | +24% | no outs seen |
| -16% | -14% | -13% | -11% | -9.6% | one out seen | |
| 44 | +31% | +34% | +36% | +38% | +41% | no outs seen |
| +6.4% | +7.8% | +9.5% | +11% | +12% | one out seen | |
| -21% | -21% | -21% | -21% | -21% | both outs seen | |
| 55 | +47% | +48% | +50% | +53% | +55% | no outs seen |
| +27% | +28% | +29% | +30% | +31% | one out seen | |
| +4.5% | +4.5% | +4.5% | +4.5% | +4.5% | both outs seen | |
| 66 | +55% | +56% | +58% | +59% | +61% | no outs seen |
| +39% | +39% | +40% | +41% | +42% | one out seen | |
| +21% | +21% | +21% | +21% | +21% | both outs seen | |
Marginal Raising Hands
The following table shows the marginal raising hands according to basic strategy, and the difference between raising 4x and checking these hands given table information concerning your outs. Note that the value of a nominal raising hand increases tremendously at a full table when not copied (all outs remain). E.g., with no other information, raising Q8o preflop instead of checking is worth about 2.3% of the Ante bet. However, at a full table (6 players), when no one has any Q or 8, then the value of raising vs. checking is +26% of the Ante. On the other hand, it is much better to check Q8o if your table is 4-handed or less, and someone has a Q or 8.
| Total Players @ Table | ||||||
|---|---|---|---|---|---|---|
| Hand | 2 | 3 | 4 | 5 | 6 | information |
| JTo | +12% | +16% | +21% | +27% | +33% | no outs seen |
| -6.8% | -1.9% | +3.0% | +7.9% | +14% | one high out seen | |
| -6.6% | -1.9% | +2.6% | +7.8% | +14% | one low out seen | |
| -26% | -22% | -18% | -13% | -8.0% | one high & one low out seen | |
| Q8o | +6.9% | +11% | +16% | +20% | +26% | no outs seen |
| -9.0% | -5.0% | -1.1% | +3.8% | +8.2% | one high out seen | |
| -9.7% | -5.7% | -2.1% | +2.6% | +7.8% | one low out seen | |
| -26% | -23% | -19% | -15% | -11% | one high & one low out seen | |
| Q9o | +15% | +20% | +24% | +29% | +34% | no outs seen |
| -0.8% | +3.0% | +7.5% | +12% | +17% | one high out seen | |
| -1.0% | +2.9% | +6.9% | +11% | +17% | one low out seen | |
| K5o | +7.1% | +9.7% | +14% | +18% | +22% | no outs seen |
| -6.9% | -3.5% | -0.1% | +3.7% | +7.5% | one high out seen | |
| -6.2% | -3.2% | +0.1% | +4.0% | +7.7% | one low out seen | |
| -20% | -17% | -14% | -11% | -7.4% | one high & one low out seen | |
| K6o | +12% | +15% | +19% | +23% | +28% | no outs seen |
| -2.1% | +1.1% | +4.9% | +9.0% | +13% | one high out seen | |
| -2.1% | +1.0% | +5.0% | +8.2% | +12% | one low out seen | |
| A2o | +16% | +19% | +22% | +25% | +29% | no outs seen |
| +3.1% | 5.8% | +9.2% | +13% | +16% | one high out seen | |
| +4.5% | +7.5% | +9.6% | +13% | +17% | one low out seen | |
| -7.4% | -5.6% | -2.9% | -0.1% | +3.1% | one high & one low out seen | |
Marginal Checking Hands
The hands in the table below are normally checking hands in basic strategy, but if none of your outs are seen by the table, they may be more advantageous to raise. The table shows the difference between raising 4x and checking these hands, given the table information concerning your outs.
| Total Players @ Table | ||||||
|---|---|---|---|---|---|---|
| Hand | 2 | 3 | 4 | 5 | 6 | information |
| T9o | -9.8% | -4.4% | +1.2% | +6.7% | +13% | no outs seen |
| J8o | -7.2% | -2.9% | +2.8% | +8.1% | +14% | no outs seen |
| J9o | +1.9% | +6.8% | +12% | +17% | +23% | no outs seen |
| Q5o | -11.5% | -7.4% | -3.1% | +1.6% | +6.5% | no outs seen |
| Q6o | -6.0% | -2.5% | +2.1% | +6.5% | +12% | no outs seen |
| Q7o | -2.7% | +1.5% | +5.9% | +11% | +16% | no outs seen |
| K2o | -9.2% | -5.0% | -0.9% | +3.7% | +8.4% | no outs seen |
| K3o | -3.6% | -0.1% | +4.2% | +8.3% | +13.1% | no outs seen |
| K4o | +1.0% | +4.8% | +8.9% | +13% | +18% | no outs seen |
2009 UTH Win/Loss Statement
I just learned that all casinos are required to provide a player with an annual win/loss statement on request. This is to provide a player with an estimate of his net win or loss at the casino for the calendar year, in case you need to write off gambling losses against a W2-G win. The casinos seem to take this regulation pretty seriously, since I see that every $100 buy-in needs supervisor approval, as does every color-out at the end of a session. The floor supervisor enters the data at the console (usually attached to the table), and everyone is tracked.
So yesterday, I was playing Ultimate Texas Hold’em (UTH) as usual, at Harrah’s, on my usual route of the four north San Diego county casinos (Harrah’s, Pauma, Pala, and sometimes Pechanga). I’d been playing exclusively UTH at these casinos for about three months now, logging in about 300 hours total. I’d been doing well, and I knew I wasn’t just donating to the casino (i.e., ATM -> UTH -> casino). So, I just decided to see if I could get my 2009 Win/Loss Statement at each of these casinos.
| Casino | Buy-In | Cash-Out | Net |
|---|---|---|---|
| Harrah’s Rincon | -$9.74 | ||
| Casino Pauma | $17,840.55 | $18,001.30 | +$160.75 |
| Pala | +$170 | ||
| Pechanga | +$300 | ||
| Total | +$621.01 |
As far as discount gambling goes, I’m claiming success. On average, I should lose about $3.50/hr ($.12/hand), so my 300 hours in 2009 should have totaled to a $1000 loss. So I’m way ahead of the mean here. Also, from what I see at the tables, I’m sure most players don’t want to see their win/loss statements for the year. That’s because most people are afraid to 4x raise preflop according to basic strategy. They’re constantly checking monsters like ATo, KJo, 66, QJo, etc. Then they still check their pairs on the flop, I guess waiting for their hands to improve at the river. They make so many mistakes, they’re probably giving the house an average 10%+ edge. They never bet their hands, and they forfeit the huge +46% Play bet edge. I just see people play passively, re-buying until they bust out. And these people are regulars, who see me all the time, but they won’t stop checking. Maybe if they read this post, they’ll start betting.
A Few Refinements for UTH Basic Strategy
I’ve been doing fine playing UTH over the last two weeks, and I’m also finding Six Card Dealer Bluff fun and fair to play. I’ve noticed that in UTH I often have a decision to call at the river with 2nd nut kicker on an unpaired board. It looked at little weird to call sometimes, especially against a board with a possible flush. So I tried out a few cases, and found that I shouldn’t call with 2nd nut kicker unless there was no possible flush, or if both my cards played. I updated this to the main Ultimate Texas Hold’em page, and the basic strategy card.
I also checked that calling 1x with 5th nut kicker against a double-paired board is okay, as long as the pairs are 7’s up or better. Otherwise, for 6’s up, you need 4th nut kicker to call.
Finally, I found that on the flop, you can bet 2x with nut kicker, as long as you have a gutshot straight draw.
ShuffleMaster’s Dealer Bluff Six Card Poker @ Pala Casino
I just tried out ShuffleMaster’s new Dealer Bluff Six Card Poker game at Pala Casino, just north of San Diego. It’s a new idea in poker-based table games, where the dealing machine knows the value of its hand, and bets against you. When I first saw this game last week, I was really puzzled. How would you play your hand? Would it cost a lot of money to figure out how aggressive the machine was? How was I supposed to analyze this game?
I looked into the details of the game, and its actually pretty simple how it all works. By its stated math, its not a bad game at around 0.5% house edge (element of risk). The player first bets an equal Ante and Blind bet. All players and the dealer are dealt six cards, from which to make a five card hand. The dealer acts first, and either checks (0x), or bets 1x ,2x, or 3x the Ante, based on its hand strength, and simple randomization. This simple randomization is stateless (independent from hand-to-hand), and uses a published wager matrix (“house-way”). The player may either fold (or check if no dealer bet), call, or raise (double the dealer bet). The dealer calls all player bets/raises. The hand is resolved just like their Ultimate Texas Hold’em game, where the Ante plays only if the dealer qualifies with a pair or better, the Play bet always gets even-money action, and the Blind bet pays only if the player wins, and according to a paytable. The game is easy to analyze, because of the simple, stateless, and published dealer betting strategy (“house-way”). Given house-way, a player basic strategy is determined, and the house edge is calculated.
The game is kind of fun, because the dealer acts first, and you benefit from this position. If you raise the dealer, it must always call (it can’t come over the top, and re-raise you). Sometimes you have easy folds, or easy raises. However, basic strategy requires you to call or raise a lot of hands, even when the dealer is betting 3x, since it bluffs a lot. This of course adds to your variance, and sometimes you’ll wonder why you had to call 3x “to keep the dealer honest”.
As usual in these ShuffleMaster games, the Ante bet is -EV because of the pair qualifier needed to pay, and the Blind bet is -EV because of the paytable. The Play bet is +EV, because you’re acting last, and the dealer must call your bets/raises, and cannot re-raise. However, the dealer may bluff, so you need to know (exactly) how the betting logic works. If you have this info (or can learn it), then the Play bet will always be +EV. The game is designed so that the sum of these 3 EVs yield a reasonable house edge.
This is why I have reservations about the game. Player basic strategy is completely dependent upon how the dealer bets his hand. ShuffleMaster goes out of its way to provide all the data on this process, and even provides the players with basic strategy and percentage tables in their literature. At Pala, there are ample supplies of this literature at the table. The dealer house-way is provided. However, if house-way should change for any reason, the player using an out-of-sync basic strategy may be severely penalized.
| dealer hand | 0x (Check) | Bet 1x | Bet 2x | Bet 3x |
|---|---|---|---|---|
| Royal Flush | 1% | 1% | 5% | 93% |
| Straight Flush | 1% | 1% | 5% | 93% |
| Four-of-a-Kind | 1% | 2% | 5% | 92% |
| Full House | 3% | 6% | 10% | 81% |
| Flush | 3% | 6% | 15% | 76% |
| Straight | 3% | 6% | 10% | 81% |
| Trips | 1% | 7% | 20% | 72% |
| Two Pair | 3% | 8% | 40% | 49% |
| High Pair (Tens – Aces) | 6% | 12% | 52% | 30% |
| Mid Pair (6’s – 9’s) | 16% | 40% | 35% | 9% |
| Low Pair (2’s – 5’s) | 26% | 50% | 15% | 9% |
| Nothing | 35% | 51% | 6% | 8% |
This table provides the percentages of the way the dealer will bet his hand, using a random number generator. No previous knowledge of the player’s history, bet amount, or anything else is used to determine the dealer’s bet.
Based on this house-way wager matrix, basic player strategy is optimized as follows:
| Dealer Bet | Fold | Call | Raise |
|---|---|---|---|
| 0x | — | — | AK or better |
| 1x | KJ6 or worse | in between | any pair or better |
| 2x | pair 7’s or worse, pair 8’s w/o kickers |
in between | pair J’s w/ kicker, or better |
| 3x | pair J’s or worse | in between | two pairs, 5’s and 3’s, w/ kicker, or better |
If everything operates exactly per these assumptions, then the house edge is only 0.5% (element-of-risk), or about 2% of the Ante bet. This is only $.10 per $5 Ante bet, and is very reasonable. However, if the dealer strategy is not exactly as described by the stateless house-way table above, the player return could be much worse. For example, the dealer cannot sub-divide the last “Nothing” row, into various sub-percentages based on A-high, K-high, etc. It’s assumed that it treats all no-pair hands the same, and applies an equal bluff probabilities to them, regardless of high card value.
What’s worse, if the dealer behaves significantly differently from the house-way table, the effect on the player using a basic strategy optimized for it could be disastrous. As an experiment, I tweaked the wager matrix to make the dealer more honest (bluff less) in a few rows, to see the effect.
First, I made the dealer more conservative with its high pairs. I shifted the majority of these bets to 1x, thereby giving the player less opportunities to come over the top with a raise to 2x, or even 6x. I modified the following single table row to
| dealer hand | 0x (Check) | Bet 1x | Bet 2x | Bet 3x |
|---|---|---|---|---|
| High Pair (Tens – Aces) | 0% | 80% | 15% | 5% |
and the results were very significant, increasing the house edge to about 5.2% (element-of-risk), or -17.8% of the Ante bet! This really surprised me. The house could (not intentionally, of course) change a few small settings, and really hurt the player relying on the published basic strategy. Unless the player could look at the stats maintained by the betting mechanism, it’s a real leap of faith to get involved with this game for any period of time.
Next, I looked at the effect of making the dealer more conservative with its nothing hand, making it check the vast majority (80%) of the time, and betting 1x the rest of the time (20%). Again, this reduces the ability of the player to just call and win with a reasonable hand, or come over the top with a big raise.
| dealer hand | 0x (Check) | Bet 1x | Bet 2x | Bet 3x |
|---|---|---|---|---|
| Nothing | 80% | 20% | 0% | 0% |
The effect of this row change was less significant, increasing the house edge to about 2.0% (element-of-risk), or -6.6% of the Ante bet. If both these row changes are applied together, the effects are additive. Of course, if the player knows about these changes, then he can modify his basic strategy to again be +EV on the Play bet. Again, since the dealer acts first, must call all player raises and cannot come over the top, the Play bet will always be +EV, given knowledge of how the dealer behaves. The above house edge effects for the wager matrix changes are based on a player using the published basic strategy.
I stopped after looking at these two simple, but significant effects. That’s all I needed to see.
Usually, I’m very naive, and always assume the casino is operating according to fair rules, and everything is on the up-and-up. However, with the advent of this new type of game, where the shuffler actually reads all hands it deals (it must, as the dealer hand is the last out of the shuffler, and the operator hits the ‘stop’ button to tell the betting logic use the last hand), I’m getting a little nervous. Also, the nature of a heads-up poker game requires knowledge of your opponent. Although ShuffleMaster provides a complete model of this opponent, its always possible that something gets lost in the process, a transcription error occurs, and/or something changes, and basic strategy gets out of sync with the actual dealer behaviour.
I think the game could be fun and safe, provided that ShuffleMaster provides a few assurances to the players. First, they need to make it extremely clear, and verify, that there’s only one version of the wager matrix. Furthermore, this can never change. Additionally, they could provide assurances to the players that the betting logic is audited by built-in stats collection in the shuffler, and periodically checked against the published, unchanging house-way. If they can provide these assurances, you can feel safe walking up to the game for the first time, and betting following basic strategy. Otherwise, while possible, it’s a pretty big task for people to figure out the dealer betting strategy, and to devise the appropriate counter-strategy. I’m just there to have fun, not to play Big Blue (that can see your cards).
ShuffleMaster Ultimate Draw Poker Machine @ Viejas
 There’s a new multi-player video “table” game at Viejas from ShuffleMaster, called Ultimate Draw Poker. (This game is different from the cards and table version of the game, which uses community draw cards.) The new Ultimate Draw machine seats up to five players, who play against a dealer hand. The game is “virtual single deck”, meaning that as far as any one player is concerned, you’re playing heads up against the dealer using a single deck. I’ll explain how they do this below.
There’s a new multi-player video “table” game at Viejas from ShuffleMaster, called Ultimate Draw Poker. (This game is different from the cards and table version of the game, which uses community draw cards.) The new Ultimate Draw machine seats up to five players, who play against a dealer hand. The game is “virtual single deck”, meaning that as far as any one player is concerned, you’re playing heads up against the dealer using a single deck. I’ll explain how they do this below.
The minimum bet (Ante) for this game is $3, and the maximum is $100. The video table is very nice, a single horizontal display for all player and the dealer hands, with nice visual effects (card animations, etc.). A vertical display is used to show a life-size dealer from the waist up, which is close enough to soft-core pornography to make you feel slightly uncomfortable. The dealer is dealt five cards face down, and also 5 replacement cards (not shown) from which she may draw. The remaining 42-card deck is then cloned for each seated player. Each player is dealt a five card hand of out a shuffled, 42-card cloned deck. The player decides what to discard, then draws from his cloned deck.
Once all players have discarded and drawn to their final hand, the dealer turns up her hand. The dealer applies a simple house-way discard policy:
- hold a pair or better, ELSE
- hold a four-card flush draw, ELSE
- hold an open-ended straight draw, ELSE
- hold all high cards (>= Jack), ELSE
- discard everything.
The dealer needs to make a pair or better to qualify. If she doesn’t qualify, you win 70% of your Ante bet. If she qualifies, then your Ante bet plays for even money against her hand.
Fortunately, “house-way” is a little weak, and a better player strategy exists (0.32% better than “house-way” vs. “house-way”):
- hold a pair of 3’s or better, ELSE
- hold a pair of 2’s unless flush draw w/ Jack or better, or unless kicker is King or better, ELSE
- hold a four-card flush draw (unless offsuit kicker better*), ELSE
- hold an open-ended straight (unless kicker better**), ELSE
- hold two highest cards >= Jack, ELSE
- hold JTs, ELSE
- hold highest card >= Ten, ELSE
- discard everything.
where:
*Ace is better than four-card flush draw, unless draw contains Queen or bettter
*King is better than four-card flush draw, unless draw contains Jack or better
**the following table shows kickers better than open-ended straight draws
| draw | min kicker to hold |
|---|---|
| 2345 | Ten |
| 3456 | Ten |
| 4567 | Jack |
| 5678 | Queen |
| 6789 | King |
| 789T | Ace |
| 89TJ | Ace |
| 9TJQ | — |
The house edge is very small for this game, only 0.61% for the above player strategy. However, the bonus bet is really bad, since it pays something like a Jacks-or-better video poker game, but you’re playing a strategy to beat the dealer hand, not to win a bonus. For the following table, and above player strategy, the bonus bet has about a 14% house edge. If you want to play the bonus bet, go find a video poker machine, it’s faster and pays more.
| Hand | Win |
|---|---|
| Royal Flush | 1000 |
| Straight Flush | 150 |
| Four Of A Kind | 25 |
| Full House | 8 |
| Flush | 7 |
| Straight | 5 |
| Three of A Kind | 3 |
| Two Pairs | 1 |
| all others | -1 |
There’s a small “collusion” opportunity in this game. Because the game is played with cloned decks, and each player acts in turn, a player acting last gets to see a lot of the 42-card cloned deck. For example, if you look at all the dealt player hands, you can see what’s available in the cloned deck (any card you see is in the cloned deck). And, when you see what’s drawn, you get more info of what’s available. There’s a few cases where this info would help you make a borderline discard decision. There’s probably aren’t enough situations like this to make it worthwhile, but I could be wrong.




2 comments