Improved Six-Card Poker Collusion Strategy (+EV)
I’ve been playing a lot of Six Card Poker at my local Viejas Casino, which gave me the chance to think about a better collusion strategy. When I first posted about this game, I was disappointed that the theoretical limit for collusion would yield only around +1.2% on the Ante bet. So I didn’t try too hard to make a good collusion strategy.
But it’s a pretty fun game, since the dealer shows half his hand, and with a full table, you’ll know 39 of the 52 cards. You can get the rules of the game from the WoOs.
After thinking it through, I boiled down the 6-way collusion strategy to the following three rules:
- fold any hand already beat by dealer
- fold any qualifying hand when there are 4 or more remaining single-card outs that beat you
- fold any non-qualifying hand when a kicker out remains that beats you, or there are 3 or more remaining pair outs for the dealer
This collusion strategy simulates at +0.43%, which isn’t bad. It’s pretty easy to count remaining dealer outs among the confederates. People just have to chime-in on how many copies of the dealer cards they have. The strategy is extremely simple, and the variance is pretty low given the 1x call, and the help in folding -EV hands.
SuperPeek Texas Hold’Em @ Suncruz Casinos
Thanks to reader K. for pointing out this obscure game available on the Suncruz Casino boats. It’s an interesting Hold’Em-based carnival game where you get to see the two dealer hole cards. Here are the rules:
- Player wagers Ante before game begins.
- Dealer reveals his two hole cards.
- Player must bet either 2x or 4x his Ante, based on the dealer’s two hole cards.
- Player receives his two hole cards, and decides to either 1x Call, or to surrender half of his 2x/4x bet (keeps Ante).
- Dealer reveals community flop, turn, and river.
- If final Player hand beats Dealer hand, the Ante and 2x/4x bet pay even-money. The 1x Call bet pays even-money for a flush or higher, else pushes.
- If the final Dealer hand beats the Player hand, all bets lose.
- Regardless of Dealer Hand, a 1x called Player hand qualifies for an automatic bonus (50:1 for Royal, 25:1 for Straight Flush, 10:1 for Quads, 1:1 for Full House and Flush).
The following strategy is within 0.61% of optimal. There are two decision points. The first decision is whether to wager 2x or 4x against the dealer hole cards. The second decision is whether to surrender half your 2x/4x bet, or to 1x call the hand and see the river.
After seeing the dealer’s two hole cards, you should:
- 2x against any dealer pair.
- 2x against any dealer Ace or King.
- 2x against a Queen, except 4x against Q3o or lower.
- 2x against a Jack, except 4x against J3s/J5o or lower.
- 2x against a Ten, except 4x against T5s/T6o or lower.
- 2x against a Nine, except 4x against 96s/97o or lower.
- 4x all others.
Once you see your hole cards, make the 1x call decision according to the prioritized strategy:
- Against a dealer pair, call two over cards or an equal pair, else surrender.
- Call any pair, except against a higher dealer pair.
- Call any hand higher than or equal to dealer.
- Call a 4x bet if you copy one card with the dealer, but the dealer’s kicker is 7 or lower.
- Call a suited hand copied once with dealer, against an offsuit dealer hand with 7 or lower kicker (e.g., call 63h against dealer 73o).
- Call two live cards when your low card beats the dealer’s low card, AND (you’ve made a 4x bet OR you’re suited OR you’re 3-gapped or less).
- Call two live cards for a 4x bet when the dealer cards are less than 9, not suited, and 3-gapped or more.
- Call two live suited cards when your high card beats the dealer’s low card, AND (the dealer is not suited OR you’re 3-gapped or less).
- Call two live suited under cards for a 4x bet when you’re 4-gapped or less, AND (the dealer is not suited OR the dealer cards are of a different suit).
- Else, surrender all others
The game is good, and you should play it if you find it.
Lucky 9 @ Harrah’s Rincon
There’s a new game Lucky 9 at my nearby Harrah’s Rincon that’s a hybrid between baccarat and blackjack. It plays like simplified blackjack, where you can only hit once, and hand totals are between 0-9. Like blackjack, you start with two cards, and the dealer exposes their top card. Like baccarat, hand values are equal to the last digit of the sum of the cards. The best hand is a Lucky 9, which is a two card 9 without a face/ten. It ties a Natural 9 (two card 9 w/ face/ten), but otherwise pays 3:2. However, Lucky 9’s after splits only pay even-money, and push against all dealer 9’s. The house edge of the game is 1.18%.
Probably, the only point of playing this game would be to see how confused the dealer gets when resolving hands involving Lucky 9, especially after split, or against a dealer Natural 9. I’m sure they’ll probably let you hit some hands after splits too. And people will think you’re crazy for standing on 5’s and 6’s.
Rules
The rules for Lucky 9 are as follows:
- Bets are placed before the hand is dealt.
- Player and dealer each receive 2 cards; the dealer upcard is exposed.
- The player may split pairs (up to 3 times) by matching the initial wager. Split hands receive only one card.
- The player may hit any non-split hand once, or stand.
- After the players action is complete, the dealer turns up his hole card.
- The dealer hits once on totals of less than 5.
- A non-split Lucky 9 (2-card 9 w/o 0-value card) pays 3:2, except for pushes against a dealer 2-card 9.
- A dealer Lucky 9 beats a player 3-card 9.
- All other player 9’s vs. dealer 9’s push.
- The player automatically loses with a total of 0, 1, or 2.
- Otherwise, wagers are resolved by comparing hand point totals.
Basic Strategy
I put the rules into my blackjack analyzer, and came up with a house edge of 1.18%, and the following auto-generated strategy:
| Hand | Dealer Upcard | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | A | |
| 2-Card Totals | ||||||||||
| 6-9 | S | S | S | S | S | S | S | S | S | S |
| 5 | S | S | S | S | H | H | H | H | S | S |
| 0-4 | H | H | H | H | H | H | H | H | H | H |
| Pairs | ||||||||||
| A-A | H | H | H | H | H | H | H | H | H | H |
| 10-10 | P | P | H | H | H | H | H | H | P | P |
| 9-9 | S | S | S | S | S | S | S | S | S | S |
| 8-8 | S | S | S | S | S | P | S | S | S | S |
| 7-7 | P | P | P | P | P | P | H | H | P | P |
| 6-6 | P | P | P | P | P | H | H | H | P | P |
| 5-5 | P | P | P | P | H | H | H | H | P | P |
| 4-4 | S | S | S | S | S | S | S | S | S | S |
| 3-3 | S | S | S | S | S | S | S | S | S | S |
| 2-2 | H | H | H | H | H | H | H | H | H | H |
The EORs for the game are extremely low compared to blackjack. There’s no value in counting this game.
Lucky 9 Bonus
The Lucky 9 Bonus is a side bet on your first 2 cards and the dealer upcard. The bet pays for various 3-card totals of 9, as listed in the paytable below. The house edge for this side bet is 13.1%. The EORs (sensitivities to card removal) are too low, and the initial house edge is too high, to make the side bet very countable. An ideal counter (using perfect knowledge of shoe composition) will find +EV betting opportunities about 2.7% of the time, with an average +10.8% EV/bet.
| Hand | Payout | Combinations | Probability | Return |
|---|---|---|---|---|
| Suited 3-3-3 | 200 | 224 | 0.000019 | 0.003761 |
| Suited 2-3-4 | 100 | 2,048 | 0.000172 | 0.017193 |
| Any 3-3-3 | 50 | 4,736 | 0.000398 | 0.019879 |
| Any 2-3-4 | 40 | 30,720 | 0.002579 | 0.103155 |
| Suited 9 Total | 30 | 70,144 | 0.005888 | 0.176653 |
| Other 9 Total | 5 | 1,070,592 | 0.089874 | 0.449369 |
| nothing | -1 | 10,733,696 | 0.901071 | -0.901071 |
| Total | 11,912,160 | 1.000000 | -0.131061 |
Counting CSM Blackjack (+EV)
A few people have asked me about the countability of blackjack dealt from a constant shuffle machine (CSM). I’m a big advocate of counting the CSM, especially for card craps, because of the ease of the windowed count. Even if the dealer collects no muck (i.e., immediately shuffles completed hands back into the CSM), you’ll still be +EV more than 8% of the time for good BJ rules. It’s a lot easier to count a CSM than a shoe. I call it counting for the ADHD crowd. All you have to do is pay attention to the last 16 cards (or the collected muck) fed into the CSM before the hand is dealt. Plus, you’ll probably never get backed off from CSM blackjack, even when wildly varying your bets.
EV vs. Windowed Count
I use my model of the ShuffleMaster 126 (source) CSM in the blackjack simulations for this post. I’ve talked in detail about this model before, in my posts on card craps. Basically, there’s a buffer of at least 16 cards in the chute (so the dealer never waits for a card), which introduces state into the system. If the dealer collects no muck, you simply use the running count of the last 16 cards fed into the shuffler. Use the simple hi-lo count (2-6 are +1, 10-A are -1). If the dealer collects a lot of muck, and feeds it all into the shuffler right before the next hand starts, then use the count of the entire muck.
For these simulations, I used 6 decks in the CSM, and typical-good H17 blackjack rules (3:2 BJ, late surrender, re-split Aces 3-times, double-after-split). My blackjack analyzer calculates the ideal EV for these rules at -0.445% for 6 decks. I ran the simulator head’s up against the dealer, and kept track of the 16-card windowed count and the subsequent hand outcome. I plotted the next-hand EV vs. the windowed hi-lo count in the graph below.
The graph shows a very linear relationship between the 16-card windowed hi-lo count and the EV of the next hand. When the running windowed count is +5 or more, the next hand from the CSM is +EV. The windowed count is ≥ 5 about 8.2% of the time.
| Count | Frequency | Approx. BJ EV |
|---|---|---|
| 0 | 11.5% | -0.44% |
| 1 | 10.8% | -0.34% |
| 2 | 9.36% | -0.24% |
| 3 | 7.46% | -0.16% |
| 4 | 5.46% | -0.05% |
| 5 | 3.67% | +0.04% |
| 6 | 2.25% | +0.14% |
| 7 | 1.25% | +0.22% |
| 8 | 0.627% | +0.29% |
| 9 | 0.280% | +0.43% |
| 10 | 0.111% | +0.49% |
Conclusions
Serious card counters will tell you you can’t count a CSM. But the data above shows that a CSM goes +EV more than 8% of the time. Plus, it’s infinitely easier to count a CSM than it is to count a shoe. You can lose track of the count for a hand or two. As soon as you regain attention, you’ll know what the count is. You can probably vary your bets wildly without attracting any attention or interest from the floor. You can probably even Wong hands when the count is bad. Or less than +5.
Counting a CSM is great for the casual counter. It’s basically short-attention span counting. If you see the last 16 cards into the CSM prior to the deal are low (have a running count of 5 or better), then you’re +EV for the next hand. Even if you just see a net +3 count for the last 16 cards, you still know the next hand will be better than average. You can start/stop paying attention on a per-hand basis (unlike a shoe, where you have to wait for the next shoe if you lose the count).
At it’s simplest, CSM counting will tell you when the next hand will be better-than-average (half the time), or worse-than-average (half the time). So, if you Wong half of the time, you’ll only play the better-than-average hands (EV better than -0.45%; the above curve to the right of count=0), and miss the bad hands. That’s a quick way to reduce the house edge from 0.45% to 0.22% (only play 53% of the hands; wait until the count is ≥ 0).
No-Bust 21st Century BJ (Ver 4.01) @ Ocean’s 11 Cardroom
They’ve changed the No-Bust 21st Century BJ rules a few times at the Ocean’s 11 Cardroom in Oceanside, CA. They’re on something called Version 4.01, with the following rules:
- blackjack pays 6:5
- re-split pairs up to 3 times, including Aces
- push on 3-card player busts of 23, 24, 25 when dealer busts with a higher total
- late surrender on first 2 cards
I ran the rules in my blackjack analyzer, which calculates the EV at -1.34%. If that’s not crappy enough, they charge an additional ≥ 1% collection on every hand. I have no idea why they would create a worse game for the player, especially when they also face the house collection. I guess the corporation bank wasn’t making enough after paying for collection and employee costs.
The WoOs lists the player cost of 6:5 blackjacks at 1.39%, which is not overcome by the “No-Bust” rule. The strategy below looks a lot like regular blackjack, with some subtle exceptions that make sense for the alternate rules.
My analyzer now outputs HMTL, which is cut-and-paste here:
| Hand | Dealer Upcard | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | A | |
| Soft Totals | ||||||||||
| soft 20/21 | S | S | S | S | S | S | S | S | S | S |
| soft 19 | S | S | S | S | D | S | S | S | S | S |
| soft 18 | D | D | D | D | D | S | S | H | H | H |
| soft 17 | H | D | D | D | D | H | H | H | H | H |
| soft 16 | H | H | D | D | D | H | H | H | H | H |
| soft 15 | H | H | D | D | D | H | H | H | H | H |
| soft 14 | H | H | H | D | D | H | H | H | H | H |
| soft 13 | H | H | H | D | D | H | H | H | H | H |
| 2-Card Hard Totals | ||||||||||
| hard 18-20 | S | S | S | S | S | S | S | S | S | S |
| hard 17 | S | S | S | S | S | S | S | S | S | R |
| hard 16 | S | S | S | S | S | H | H | H | R | R |
| hard 15 | S | S | S | S | S | H | H | H | H | H |
| hard 14 | S | S | S | S | S | H | H | H | H | H |
| hard 13 | H | S | S | S | S | H | H | H | H | H |
| hard 12 | H | H | S | S | S | H | H | H | H | H |
| hard 11 | D | D | D | D | D | D | D | D | D | D |
| hard 10 | D | D | D | D | D | D | D | D | H | H |
| hard 9 | H | D | D | D | D | H | H | H | H | H |
| hard 5-8 | H | H | H | H | H | H | H | H | H | H |
| Pairs | ||||||||||
| A-A | P | P | P | P | P | P | P | P | P | P |
| 10-10 | S | S | S | S | S | S | S | S | S | S |
| 9-9 | P | P | P | P | P | S | P | P | S | S |
| 8-8 | P | P | P | P | P | P | P | P | P | P |
| 7-7 | P | P | P | P | P | P | H | H | H | H |
| 6-6 | P | P | P | P | P | P | H | H | H | H |
| 5-5 | D | D | D | D | D | D | D | D | H | H |
| 4-4 | H | H | H | P | P | H | H | H | H | H |
| 3-3 | P | P | P | P | P | P | P | H | H | H |
| 2-2 | P | P | P | P | P | P | H | H | H | H |
Ultimate Three Card Poker (Face Up)
Thanks to reader Jet for pointing out this new ShuffleMaster ™ game. I ran a quick analysis this morning to check his numbers, and of course to check for any collusion possibilities. An optimal strategy yields a -3.8807% return, and we pretty much came up with the same basic strategy (differences arise from suit assumptions). You should 3x raise all pairs or better, and 1x call according to the following table.
An ideal collusion simulation with 6 confederates yielded no practical gain 😦 This probably makes sense, because you can’t really take advantage of collusion information when they limit 3x raises to pairs. Perhaps you can get a slight edge on some 1x/fold borderline cases, but it doesn’t amount to anything significant.
Jet has a hole-carding strategy that yields 9%, which you can contact him for.
| Dealer Upcard | Min Calling Hand |
|---|---|
| 2 | 98x |
| 3 | Txx |
| 4 | T4x |
| 5 | T5x |
| 6 | T6x |
| 7 | T7x |
| 8 | T6x |
| 9 | Txx |
| T | T84 |
| J | J84 |
| Q | Q84 |
| K | K84 |
| A | A85 |
Free Bet Blackjack @ Golden Nugget, LV
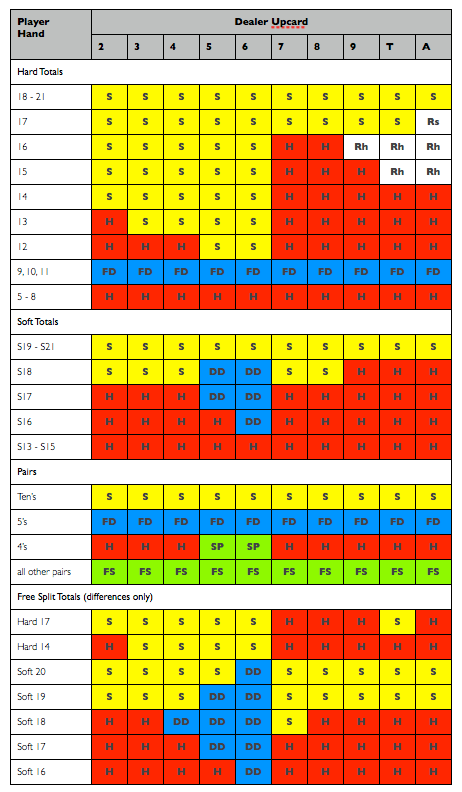
Well, the tables are turned around, and now it’s me that’s on the hook for the house edge in a new game. I did the analysis for Geoff Hall’s (the inventor of Blackjack Switch) new Free Bet Blackjack. The game just went live at the Golden Nugget in downtown Las Vegas this week, and everyone is on edge that the game performs as calculated. There were a lot of winners on Wednesday, and because the game seems so crazily liberal, people were concerned (including me). So, I double checked all my work today, and while I found a few small things in the report (**ahem**), everything seems to check out. Basic strategy simulations are running at a 0.64% house edge, vs. my calculated optimal strategy 0.625%.
Ok, here’s why the game is crazy. The game is called “Free Bet” Blackjack, because you get free doubles on any hard 9, 10, or 11, and free splits on all pairs except 10’s and 4’s. What that means is that instead of paying for a double (say on a 3-card 11), the dealer will give you “free play” chips, matching your original bet, to wager. The same applies for “free” splits. Plus, you get up to 4 free re-splits, and you also get free doubles after free splits. So you can have like 7 free bets in the game (and only 1 real bet at risk). If you win the hand, the dealer pays all the free play with real money. If you lose the hand, you only lose your original bet. The dealer retrieves all the free bets at the end of the hand. Of course, the “catch” is that it’s a 22-push game. But overall, it works out very well for the player, since you are generally not at risk for your doubles and splits. You might push more hands than you like, but it beats the dreaded “losing (all) your doubles”.
You can see how it’s possible to have a nice run in the game.
Here’s the specific rules:
- Free double anytime on hard 9, 10, or 11.
- Free splits on all pairs except Tens and 4’s
- Up to 4 free re-splits, including Aces
- Free double after (free) split
- Normal double on any two cards, including after (free) split
- Late surrender (no longer?) available on first two cards
- Blackjacks pay 3:2
- Dealer 22’s push
- 6 deck shoe
They initially offered late surrender, but we told them it brought the house edge down by 0.21% (huge). I don’t know if they took it away yet. If allowed, late surrender on 15 vs. T or A, on 16 vs. 9, T, A, and on 17 vs. dealer A.
Here’s the basic strategy generated by my analysis program. Note you treat free splits differently than normal hands. This is because you can’t lose any real money by hitting hard-17 against a dealer 7 upcard, so you might as well try to improve your hand (given push-22, and push-17 yields nothing on the free bet). Also note the regular doubles for free-split soft totals. It’s worth it to risk a real-money double rather than just hitting a free hand. These exceptions are listed in the bottom part of the strategy chart.
Basic Strategy for Free Bet Blackjack (6 Decks).
where FD = free double, FS = free split, DD = double down. Note that you take all your free doubles, and all your free splits.
I have to admit I overlooked a small rule until this morning (**ahem**), but everything is now fixed. Luckily, the numbers still worked out. This is my first time doing the math for a live game on the floor. I was slightly nervous today 🙂
7 Up Baccarat @ Marina Bay Sands, SG
In today’s Grail quest, I took a look at the countability of a Baccarat variant called 7 Up Baccarat, dealt out of a constant shuffle machine (CSM). If you’ve read this blog closely, you know that a CSM does not eliminate all countability in a game. This is because cards are in buffered in the exit chute of the CSM, so recently dealt cards have no chance of coming out soon. A windowed count may be effective against a CSM.
You can browse or download all the code for this post, if you want to see how I roll.
Anyway, here’s what I found for 7-Up Baccarat. Both the banker and player bets have very high sensitivities to removed cards (EORs). (Compare this to normal baccarat, where the EORs are effectively zero.) Simulations show a windowed count is strongly correlated to the EV of the next hand dealt out of the CSM. The figure below shows a 20-card windowed count tells you when its better to bet Player or Banker. Unfortunately, the count almost never gets good enough to be +EV. You can see if they made the game more “fair” (house edge only 1.3% instead of the chosen 2.6%), then you’d often find some +EV opportunities. I doubt they did this kind of analysis, but who knows.
Same thing with the Super-7’s side bet. If they made the nominal house edge closer to 5% than the 8.9% they chose, then it’d be very countable. The count is very simple. Any 7 you see is -12, and any non-7 is +1. I think everyone can imagine that it’s better to bet the Super-7’s when they haven’t seen any 7’s out of the CSM in the last few hands. And I’m sure no one bets Super 7’s just after seeing a bunch of 7’s come out. Simulation of the Super-7’s bet show a perfect linear correlation between the count and the EV of the bet. In all simulations, a minBufferDepth of 20 was used (minimum number of cards in the exit chute buffer).
Power98 Baccarat @ Marina Bay Sands, SG
A few months ago, a reader contacted me about the ridiculously beatable Banker/Player Natural 8/9 bets in the Power98 Baccarat game at the Marina Bay Sands in Singapore. They used to pay 10:1 on a Natural 9, and 11:1 on a Natural 8. (And, they’d pay even more on a “Power Hand”.) Needless to say, this was obviously way too countable, and they finally figured it out, and lowered the pays down to 8:1 for both bets. This game was so beatable, I was even thinking about taking a trip out there. Oh well, our reader tells us that players figured it out, followed by management, and now it’s gone. I mean, this one was old school beatable. Throp and Walden wrote about this one in 1966, and that’s with a payout of 9:1 for both bets. What were these Power98 guys thinking? Anyway, even with their dealing procedure of placing 2 decks behind the cut card, the game was still beatable for about 61% of a fixed bet per shoe. It must have been funny to see everyone all of a sudden betting huge on both Player and Banker Natural 9. Oh well, sic transit gloria.
Field of Gold (+EV)
Everybody thank Eliot Jacobson for working for you. He emailed me this morning telling me the Field of Gold blackjack side bet was crushable. And it is. For real. The count is simple, and for a 6-deck shoe game, you’ll be able to bet 19% of the time, with an average edge of +6.5%/bet. That’s a profit of ($25 bet)(19% bet/hand)(+6.5% EV/bet) = $0.31/hand. For double-deck, the numbers are even better, yielding 27% betting opportunities with an average edge of +8.2%/bet. For $25 bets, that yields a profit of $0.55 per hand dealt. That adds up pretty quickly. It’s more than $100/hr.
This is about as good as it gets, as it’s a fast blackjack game. Oh, by the way, Eliot also brought you the equally crushable Lucky Lucky bet, which I probably understated in my post. These are probably the best two countable side bets out there, and nobody but Eliot has noticed them. Oh, and he’s the one that pointed out the Dragon-7 vulnerability.
Anyway, here’s what you’re looking for:
Use the following count:
| Card | Value |
|---|---|
| Ace | -3 |
| Deuce | -1 |
| Nine, Ten, Queen, King | +1 |
| others | 0 |
Bet when the true count (= runningCount/decksRemaining) is 2.2 or better. You can see from the graph below that the EV is strongly correlated with the true count.
This side bet becomes highly profitable when the shoe is rich in aces and deuces, and lean in high cards. During some shoes, the deck can easily get really good, or really bad for the Field of Gold bet. The distribution of the side bet EV is plotted below over the course of the 6-deck shoe and the double-deck game. Note the peak of the distribution is centered about the nominal -5.66% return of the bet right after the shuffle. Then, especially towards the end of the shoe, the side bet return can vary wildly. Note all the area under the long tail of the distributions to the right of the y-axis (EV>0). This is why the game is crushable.
(5 deck penetration of 6-deck shoe; 29 cards behind cut card in double-deck.)
Discount Gambling 
leave a comment