Free Rides @ Mississippi Stud (Barona Casino)
The Social Wagering at Barona gets better and better. Unlike other casinos, Barona is fine with players passing chips around and betting on each other’s hands, and even promotes it. So, at the Mississippi Stud game, not only do you get to see all the player’s hands face up (player edge > +1.5%), you can take additional +EV bets when the hand owner doesn’t utilize his 3x bet. (E.g., small pairs with 2 trip outs on 3rd St., 6 high outs on 3rd St., flush draws on 5th St., etc.)
Last night I realized there’s an additional way to squeeze out some more EV from the game. Often, there’s players at the table that like to over-bet other people’s hands. They often want to piggy-back another 1x or 2x bet on your hand, when the correct decision is just to 1x bet the street. In this case, let them bet on your hand, but remove your own 1x bet on that street. This way, you see the street “for free” (well, the EV improvement is only around 15%). It also helps you preserve your capital, which is very important while you wait for a winner.
For example, say you have KJo, and someone else has a Jack. You’re offsuit, and have 5 high (winning) outs. You’re only supposed to 1x bet 3rd Street. But depending on the table, someone might want to “bet on your hand”, and piggy-back a 1x or 2x bet on your 3rd St. If they pass you the money, place their bet, and then remove your own. This way, you see 3rd St. “for free” (actually, you only save about 13% of the Ante in this case). While your hand is actually +EV (+.64), it’s not good enough to 3x bet (+.43, for higher risk). If someone else bets your 3rd St. for you, your EV goes up to +.77.
Or, say you have a small pair (e.g., 55). You see one of your trip outs, so you only 1x bet 3rd Street. But someone wants to gamble, and add 1x to your 3rd St. bet. Go ahead and place their bet, but remove your own. In this case, you’ll save about 14% of the Ante. The hand will return +.31 for a 1x bet, but increases to +.45 if someone else bets your 3rd St. for you.
In general, any time you’re only supposed to bet 1x, but someone wants to bet on your hand, book their action but don’t bet your own money. This way, you get to “check” through the street, and only bet when you should. This happens quite often when people are winning and having fun.
I haven’t started doing this, but I suspect people might slow down when they see you’re not willing to bet your own hand. For example, I always offer to give away my hand before I fold it. That means they can take over the hand, if they want it, for “free”. They used to snap up the offer, but lately, they all pass. They’ve either figured out the true EV of a hand, or simply realize that if I don’t want it, they shouldn’t either.
Any way, there’s just more and more +EV opportunities at the already +EV Mississippi Stud game @ Barona. Now if only they brought the Party Pit to pit 3 …
Triple Attack Ace Count Effectiveness
To graphically demonstrate the large +EV advantage obtained by a simple Ace count in Triple Attack Blackjack, I compared the EV frequencies at the 1/2 shoe depth to normal blackjack using the hi-lo count. The graph below shows the Triple Attack edge dominates that of normal blackjack. The edges obtained in Triple Attack are both larger, and more frequent than in standard blackjack. The Ace count in Triple Attack is much simpler to track, compared to the hi-lo count, because you only have to identify one card — the Aces. The graph clearly shows that if you’re going to count at a shoe game, you should play Triple Attack. (Compare the areas under the curves, to the right of EV=0.)
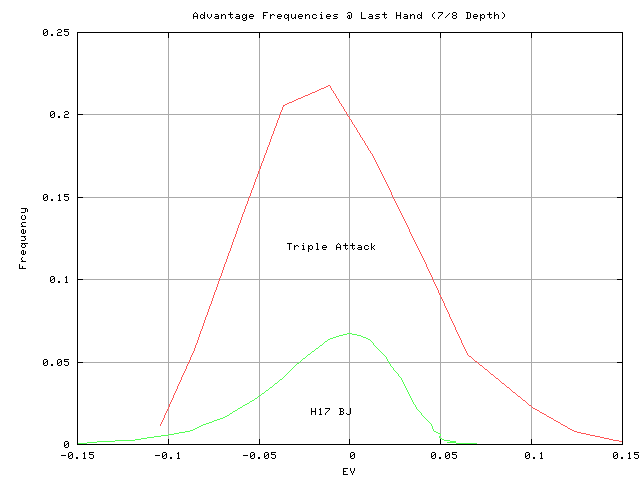
And for the last hand in the shoe:
Triple Attack BJ Session Outcome Distributions
For anyone interested in grinding out a profit from Triple Attack Blackjack, I thought I’d post a few graphs showing the distribution of outcomes for playing 100 shoes. I assumed a penetration of 7/8ths of the shoe, and for a heads-up player shamelessly betting 10x/20x when the Ace count is good, but otherwise playing basic strategy. These graphs should not be used to estimate bankroll requirements, but just give an idea of what to expect in the medium-run, and what kind of average profit rate to expect.
For a 10x big bet when the Ace count is good (+2 after 2 decks):
Note the bias in the distribution clearly favors the player counting Aces. The x-axis is the net win/loss in small (1x) bets. The curves clearly cross the 50% cumulative frequency in positive net territory.
For a 20x big bet when the Ace count is good (+2 after 2 decks):
Of course, you can also see the potentially large swings, which discourages all but extremely serious gamblers from trying this sort of thing. For example, varying your bet 20x against a unit $5 minimum bet means betting nickels when the count is bad, and black ($100) when the count is good. Over a 100 shoes, there’s a 10% probability of ending up stuck $6000 or more. Of course, there’s a greater chance of winning $6000 or more, and you’ll “average” a win of (250 units)($5/unit) = $1250 for this 100 shoe “session”.
In the next post, I’ll compare Triple Attack to normal 6-deck blackjack, showing how much more effective counting is, as far as shoe games go.
Triple Attack Blackjack (+EV) @ Barona Casino, CA
 My nearby Barona Casino opened up a new Triple Attack Blackjack game last month, and I tried it out this weekend. I really like this game, because of the weird, aggressive hitting like Spanish 21. But more importantly, the game allows you to double your initial bet after seeing your first card, and bet again after seeing the dealer upcard. You’re immediately paid on 21 or any 6-card total, and you can double down at any time. The house gets its advantage by paying even money on blackjack, and pushing on dealer 22.
My nearby Barona Casino opened up a new Triple Attack Blackjack game last month, and I tried it out this weekend. I really like this game, because of the weird, aggressive hitting like Spanish 21. But more importantly, the game allows you to double your initial bet after seeing your first card, and bet again after seeing the dealer upcard. You’re immediately paid on 21 or any 6-card total, and you can double down at any time. The house gets its advantage by paying even money on blackjack, and pushing on dealer 22.
For the full rules and basic strategy, see the Wizard’s analysis, which yields a 1.18% house edge. But for most cases, his basic strategy charts boil down to the following simple rules:
- If your first card is an Ace, triple your bet.
- If your first card is a Face, triple your bet against 2-9, else double your bet.
- 3rd Attack 2 against a 6.
- 3rd Attack 8 against 6,7.
- 3rd Attack 9 against 5,6,7,8.
- Double 10 against 3-6.
- Double 11 against 7 and under.
- The only soft total double is soft-18 against a 6.
- Double all 5-card 14’s and under.
- Double-for-less (split aces rescue) soft-17 and under, and soft-18 against 9 and A.
- Hit all 12’s and 13’s.
- Hit 14 except against a 6.
- Hit 15 against a 2 or 3.
- Hit 16 against a 2.
- Hit 17 against an Ace, and for some 5-card totals.
- Never split 4’s, 5’s, 6’s, 10’s.
- Split 2’s and 3’s against 6,7.
- Split 7’s against 4-7.
- Split A’s and 8’s against everything except A.
- Split 9’s against 6,8,9.
I really enjoyed the game. I also won about $400 in 3 sessions, which is unheard-of for me, since I flat bet for the minimum $5. I never vary my bet. However, in Triple Attack, you often end up betting 3 units, or even 6 or more, if you split hands like Aces. I don’t think I’ve ever won that much money playing blackjack before. The players all loved it, because they make more decisions, and their initial $20 bet can easily become a $120 bet on a good hand, or just remain a $20 bet on a weak hand.
Of course, it immediately occurred to me that card counting should be more effective in Triple Attack compared to standard blackjack. While you might dramatically increase your bet for a good count in regular blackjack, in Triple Attack, you only have to commit 1/3 of this amount on the 1st Attack, then another 1/3 only if you like your first card (an Ace or Face), and another 1/3 only if you like the dealer upcard. So, even though the count may be good, you can get away from a bad hand on the first card, and also if the dealer has a good upcard. Compare that to normal blackjack, where you bet huge on a good count, then get a 6, then the dealer shows an Ace.
Using basic strategy, I looked at the EV sensitivities of each of the card ranks (i.e., the effect of removing one card from the shoe). Interestingly, the effect of removing a Face card was very small. Removing a 5 improved the hand EV the most, but not by much compared to a 2, 3, 4, 6, or even a 7. By far, the Ace was the most powerful card, making the other cards insignificant.
So, I tried out a simple scheme, which only relies on the Ace count, compared to the expected number dealt. You subtract the number of actual Aces seen from the expected number of Aces dealt to get the Ace count. For example, after dealing 1/2 the shoe (192 cards), you should have seen 16 Aces. If you’ve only seen 12 Aces, then the count is +4. The Ace count is a measure of the “extra” Aces left in the shoe. Using a basic strategy simulator, I generated the curves showing the effectiveness of this simple Ace-Count system (including double-1-unit-for-less as Ace-split rescue):
This effect is huge! Look at the green curve, which shows the effect of the Ace count after 3/4 of the shoe has been dealt (288 cards dealt). At this point, 24 Aces should have been dealt, on average. But if only 20 Aces were dealt, then the count is +4, and the next hand has a 4% player advantage. Similarly, a negative count tells you to bet the minimum, or even Wong (sit out) until the next shoe. The blue curve shows the effect after 1/4 of the shoe dealt (96 cards), and the red curve shows the half-way point (192 cards). You can see that generally speaking, it’s good to increase your bet any time the count is +2 or more (the shoe is “loaded” with 2 or more extra Aces).
We don’t need to look at the distribution of Ace counts to know that +1, +2, +3, +4, +5 counts happen all the time, especially at the end of shoe, where the effect if largest. Note that the green curve shows about a 1.25% EV improvement for each surplus Ace left in the shoe.
A simple counting strategy bets the minimum for the first 2 decks of the shoe, then a large bet if the Ace count is +2 or better. Using basic strategy, and assuming the cut card at 48 cards left in the shoe, the following returns are obtained:
| Small Bet | Large Bet | Return (relative to small bet) |
|---|---|---|
| 1x | 1x | -1.10% |
| 1x | 5x | +0.08% |
| 1x | 10x | +1.60% |
| 1x | 20x | +4.40% |
| 1x | 30x | +8.80% |
| 1x | 40x | +11.8% |
On the other hand, the shoe is +EV about 20% of the time (+2 or better count) after the first 1/4 of the shoe is dealt. So, if you just like varying your bet on a good count, you’ll really enjoy this game. Overall, if you Wong and only bet +EV Ace counts, then you’ll extract about +17% total EV out of a shoe (i.e., +0.17 bets/shoe). The Ace-count system is very easy to implement (e.g., use the height of muck cards to estimate the expected Ace count), and is very fun. Some people have a good idea of when the shoe is Ace-rich or not. That’s all you need to know for this Triple Attack game!
And there’s no time to (possibly) bet big like the last hand of the shoe (purple curve, cut card @ 1 deck left):
Note that unless the Ace count is 0 (unlikely, only 22% of the time), you’re either a big favorite, or a big underdog on the last hand. It’s easy to get the Ace count right on the last hand, assuming the cut card was placed with 48 cards behind it. At the last hand, you should have seen 28 Aces. If you only saw 24, then you have a +4 count, and the EV of the next hand is almost 10% in your favor (a $100 1st Attack bet will return a $9.80 profit on average, including possible 2nd and 3rd Attacks, doubles, etc.). But, if you saw 30, then the count is -2, and the house has a 6.2% edge on the last hand, so bet the minimum, or Wong.
I suggest you simply count the number of Aces seen, even using chips if it helps you keep track. Compare your Ace count to the number of decks (48 cards/deck) seen in the muck rack. There are 4 Aces per deck. If the number of Aces seen is less than 4*(mucked decks), then the Ace count is positive. If your count is +2 or better, you’re +EV, and can increase your 1st Attack bet.
Get an idea of what a deck (48 cards) looks like in the discard rack. Ask the dealer for their estimate of the number of decks in the muck. You’ll find it’s pretty easy to estimate the number of dealt decks. Thus, you should be able to determine the Ace count very easily. Also, by watching the level of cards in the discard rack, you’ll know how powerful your count is (see above graphs for 1/4, 1/2, 3/4, and 7/8 shoe dealt depths).
Example: You look at the discard rack, and it looks like 3 decks have been dealt. This means that 4*3 = 12 Aces should have been dealt. Your actual Ace count is 15. The Ace count is -3, and you’re -EV, so bet the minimum. However, if the actual Ace count is only 9, then the Ace count is +3, and you’re +EV, so you should bet more.
This counting system couldn’t be any easier, or any more powerful. It doesn’t get much better than this.
Finally, I saw that at request, Barona increased the limits on the Triple Attack game to $25-$1000. I was locked out until the guy left, and the table returned to $5-$1000. In general, Barona is very flexible about increasing table limits.
Mississippi Stud @ Barona Casino (Update)
 I’ve been playing more full-exposure Mississippi Stud at my nearby Barona Casino, since it’s the closest casino to me, and the game is nice and full most every night. The game is a lot more fun now, since I’ve learned all the decision points of the +EV strategy. Most every hand is a “no-brainer” now, and I only have to look at my chart for some copied, suited hands.
I’ve been playing more full-exposure Mississippi Stud at my nearby Barona Casino, since it’s the closest casino to me, and the game is nice and full most every night. The game is a lot more fun now, since I’ve learned all the decision points of the +EV strategy. Most every hand is a “no-brainer” now, and I only have to look at my chart for some copied, suited hands.
I’ve fine-tuned the strategy a bit, it now simulates at a +1.85% player’s edge for a full table. I’ll publish the full strategy when I’ve finished optimizing it. I’ve computed the “element-of-risk” (return per average bet risked), and it’s an amazing +0.78%. This results from the ability to 3x bet multiple streets at no risk (i.e., the hand either pushes or wins). The “element-of-risk” figure is the more accurate indicator for games requiring post-Ante bets. This means that after your Ante, you only risk another 1.35 units per hand. That’s pretty low, considering there are 3 streets to bet.
Strategy Details
The discussion below elaborates on the +EV strategy card shown in the original +EV Mississippi Stud @ Barona post. This post clarifies a few of the decision points, and shows you how to use additional information, like high cards seen, and flush cards seen.
3rd Street
Raising Hands
There are a few hands you should 3x raise on 3rd Street, that on average will pay off better than just 1x calling. Notice that the expectation value (EV) is positive and higher for 3x raising vs. 1x calling for the following hands:
| Hand | 1x EV | 3x EV | Improvement |
|---|---|---|---|
| 6 high outs (suited) | +1.93 | +2.16 | +0.23 |
| 6 high outs (offsuit) | +1.48 | +1.55 | +0.07 |
| 6 high outs (QJo) | +1.58 | +1.71 | +0.13 |
| 5 high outs (possible straight flush) | +1.44 | +1.49 | +0.05 |
| small pair, no copies | +10.7 | +13.3 | +2.6 |
Those are the only raising hands. Bet other hands 1x at most. I often see people raising 5 offsuit high outs. That’s a losing move, as a 1x bet has a +0.63 return, while raising the bet to 3x decreases the return to +0.43. So you’re risking more and winning less. You win more by betting less. Don’t raise any hands except the ones in the above table!
Piggyback Bets
Often, people don’t 3x bet their hands on 3rd Street in the above table. Barona etiquette allows other players at the table to piggyback on the betting spot, if it’s not maxed out (3x). I take as many of these bets as I can, because they’re +EV. First, I tell the owner of the hand to max out their own bet, that it’s in their favour to do so. Only if they won’t make the bet themselves, do I ask to ride along a 2x bet. Usually, I talk people into taking their own EV. But, if they’re too scared, I’ll take the bet myself. From the above table, we see that the return for a 2x piggyback bet is the Improvement value. E.g., if someone doesn’t raise their uncopied small pair, a 2x piggyback bet returns +2.6 Ante average win, or a (2.6-2)/2 = +30% average profit. The returns are smaller for other hands, but is pretty good for 6 high suited outs (+11.5% for a 2x piggyback).
Calling Hands
| Outs | 1x EV | Notes | ||
|---|---|---|---|---|
| High | Mid | Low | ||
| 3rd Street (Offsuit) | ||||
| 3 | 0 | – | -0.47 | Call |
| 2 | 2 | – | -0.79 | Call |
| 2 | 1 | – | -1.09 | Fold* |
| 2 | 0 | 3 | -1.05 | Fold* |
| 1 | 3 | – | -0.99 | Call* |
| 1 | 2 | – | -1.31 | Fold |
| 0 | 5 | – | -0.71 | Call |
| 0 | 4 | – | -1.12 | Fold* |
| 0 | 3 | 3 | -0.95 | Call |
| 0 | 0 | 6 | -1.43 | Fold |
| 3rd Street (Suited) | ||||
| 2 | 0 | – | -0.87 | Call |
| 1 | 2 | 0 | -0.96 | Call* |
| 0 | 4 | – | -0.75 | Call |
| 0 | 3 | 3 | -0.71 | Call |
| 0 | 3 | 2 | -0.98 | Call* |
| 0 | 0 | 6 | -1.20 | Fold** |
Notes:
* EV varies +/- 0.20 depending on if the hand “reaches” (can make straight), and if less than 4 high cards are seen, and if suited, whether 3 or more flush cards are seen.
** You should call 54s if you can make a straight flush, and you’re not copied, and at most one flush card is seen.
So, you should use the above table as a guideline for calling or folding. Marginal hand (*) decisions depend on whether it “reaches”, the number of flush cards seen (< 3), the number of high cards seen (<= 4), and whether a straight flush is possible. For simplicity, treat each factor equally in making your decision. (A hand is more valuable when less than 4 high cards are seen, because it increases the probability of making a high pair on board).
4th Street
Raising Hands
| Hand | 1x EV | 3x EV | Improvement |
|---|---|---|---|
| low pair w/ all 5 outs | +1.41 | +1.67 | +0.26 |
| at least 7 or more high outs (suited) | +1.06 | +1.22 | +0.16 |
| at least 3 high outs and possible straight flush | +3.05 | +3.85 | +0.80 |
Calling Hands
The 4th Street calling points are pretty simple, and basically boil down to the following minimum hands:
- 3 high (“pay”) outs
- 2 high (“pay”) outs, and 3 mid (“push”) outs
- 1 high (“pay”) outs, and 5 mid (“push”) outs
- 6 mid (“push”) outs
You should also call a straight draw if just below these minimum requirements.
5th Street
The 5th decision is very easy to compute, since you’re betting on one card, and you know all your outs. Refer to the strategy card for the decision points, but your basic “calling hands” are
- 5 (or more) “pay” outs
- 4 “pay” and 2 “push” outs
- 3 “pay” and 4 “push” outs
- 2 “pay” and 6 “push” outs
- 1 “pay” and 8 “push” outs
These minimum calling hands are pretty easy to remember. I know that once I have 5 high (“pay”) outs, I’m never folding. Or, once I have 4 high (“pay”) outs, I only need to pick up 2 mid (“push”) outs to not fold. And, when I only have 3 high (“pay”) outs, I know I need at least 4 mid (“push”) outs to see 5th street. If my hand is worse than these minimums, on average, I’m better off folding the hand, and losing 3 units, than playing and losing more than 3 units.
| Outs | 1x EV | Notes | ||
|---|---|---|---|---|
| High | Mid | Low | ||
| 5 | 0 | – | -2.72 | Call |
| 4 | 2 | – | -2.95 | Call |
| 4 | 1 | – | -3.05 | Fold |
| 3 | 4 | – | -2.95 | Call |
| 3 | 3 | – | -3.05 | Fold |
| 2 | 6 | – | -2.95 | Call |
| 1 | 8 | – | -2.95 | Call |
You’re getting a lot of odds for the 5th Street bet, so if you feel like it, you can call with a slightly subpar hand (like short one mid out), since it only costs you 5% of an Ante on average. At a $5 Ante, that’s $0.25, so it won’t kill you to play an occasional underdog. Usually, I make the fold, but offer my hand to anyone at the table. Usually, someone wants it, because they’re getting odds for a cheap price ($0.25).
You should 3x raise any flush. It is extremely rare that any flush draw is -EV, so raise them all.
You should refer to the strategy card to know when to raise a straight draw. If all 8 straight outs are available, 3x raise the draw. Else, check the strategy card, which shows you the minimum requirements in order to raise a draw. E.g., you can raise a gutshot (4 straight outs) when you also have 8 high (“pay”) outs and 3 mid (“push”) outs.
Improved Table Rules
If you didn’t think it could get any better, Barona now lets you bet on multiple hands simultaneously. I guess this is part of their Social Wagering concept. Also, the table limits are $5-$100, with no limit on aggregate payout. So that means you can bet $100 Antes on 6 spots, with an EV of (6)($100)(1.8%) = $10.8/hand. If you get a fast table, you could play 40 hands/hr, for an average profit of $432/hr.
Simplified +EV Collusion For WPT-3x All-In (4 Players)
 I cleaned up my +EV collusion strategy for the World Poker Tour 3x All-In Hold’Em casino table game, because my old strategy was basically unplayable. I’ve simplified the strategy to focus on copied cards, and to ignore the high cards that only slightly lower the probability of the dealer qualifying. I optimized the strategy for four players, since I wanted a +EV worth playing for.
I cleaned up my +EV collusion strategy for the World Poker Tour 3x All-In Hold’Em casino table game, because my old strategy was basically unplayable. I’ve simplified the strategy to focus on copied cards, and to ignore the high cards that only slightly lower the probability of the dealer qualifying. I optimized the strategy for four players, since I wanted a +EV worth playing for.
I always see the game at the Bellagio, when I walk through it on my way to the Forum Shops at Caesar’s. It’s also dealt at my local Sycuan Casino. I always tell my friends we should play it, but no one has any interest in +EV play, or carnival games. I figure someone out there sees the value in sharing hole card info for this game, since it starts with a mere 0.74% house edge. The following simplified collusion strategy simulates at a player advantage of about 0.31%.
The game is really simple, and other than the bad bonus bets, is not very exciting. Each player posts an Ante to start the game. The player then receives 2 down cards, which combined with the 5 card board, makes a Hold’Em poker hand. The dealer also receives two down cards, for his Hold’Em hand. You look at your 2 down cards and decide to either 3x raise “all-in”, or fold and lose the Ante. Once the players action is complete, the dealer turns up his hole cards. The dealer hand qualifies if it’s a pair, or has a blackjack value of 11 or greater. If the dealer doesn’t qualify, the remaining players win the Ante bet, and the 3x Raise bet pushes. If the dealer qualifies, then he deals the flop, turn, and river. The dealer’s Hold’Em hand is compared to each player’s Hold’Em hand. If the player has the higher hand, he wins even money on the Ante and the 3x Raise. If the dealer has the higher hand, the player loses both bets. If the hands are equal, the bets push.
The basic strategy is very simple. You’re supposed to 3x raise any pair or suited hand. The only hands you fold are 23o thru 28o, and 34o, 36o, and 37o. (That’s deuce-trey thru deuce-eight offsuit, and trey-four, trey-six, and trey-seven offsuit.)
The collusion strategy is also very simple. You 3x raise anything, unless you’re copied. Fold a weak hand (the basic strategy folding hands) if copied. Slightly stronger hands are still played if only copied once. You always play a Jack or better.
If four players share down card info, then the players have about a 0.31% edge over the house. The players need to know if their hole cards are copied by their neighbors. Here’s the modified strategy:
| Hand | Basic Strategy | 4-Player Strategy |
|---|---|---|
| Offsuit | ||
| 23o thru 28o | Fold | 3x Raise if no copies |
| 29o, 2To | 3x Raise | 3x Raise if no copies |
| 34o, 36o, 37o | Fold | 3x Raise if no copies |
| 35o | 3x Raise | 3x Raise if no copies |
| 38o | 3x Raise | 3x Raise if no copies |
| 39o | 3x Raise | 3x Raise if ≤ 1 copies |
| 3To | 3x Raise | 3x Raise if ≤ 2 copies |
| 45o | 3x Raise | 3x Raise if ≤ 2 copies |
| Suited | ||
| 23s thru 28s | 3x Raise | 3x Raise if no copies, or 1 copy and ≤ 1 suit seen |
| 29s, 2Ts | 3x Raise | 3x Raise if ≤ 1 copies, or 2 copies and ≤ 1 suit seen |
| 34s thru 37s | 3x Raise | 3x Raise if no copies, or 1 copy and ≤ 1 suit seen |
| 38s | 3x Raise | 3x Raise if ≤ 1 copies, or 2 copies and ≤ 1 suit seen |
| 39s | 3x Raise | 3x Raise if ≤ 1 copies, or ≤ 1 suit seen |
| 3Ts | 3x Raise | 3x Raise if ≤ 2 copies, or ≤ 1 suit seen |
Additionally, you should fold triple-copied offsuit hands T2 thru T6, 92 thru 96, 82 thru 85, 72 thru 76, 62 thru 65, and 54.
Simplified Collusion For Mississippi Stud
When I play Mississippi Stud at the casino, I use a simplified collusion strategy that’s easier to remember than my full advanced strategy. The simple strategy only needs knowledge of your high and mid outs. It’s very easy to track them, once you know your starting outs (you have to ask around at the start of the hand). The full strategy uses low outs for the 3rd and 4th Street decisions, and uses detailed tables for 3x betting straight draws on 5th Street. The simplified strategy is very simple to remember, and still returns a positive expectation (+EV) for a full table of 6 players.
Simplified Collusion Strategy
The following simplified collusion strategy returns about +0.5% for a full table of 6 players. That’s more than a 5% improvement over playing without info (-4.91% house edge).
- 3rd Street
- small pair: 3x bet if 0 copies, 1x bet if 1 copy, fold if 2 copies
- 3x bet 5 high suited outs, or 6 high offsuit outs
- if suited, 1x bet at least 2 high outs, or 4 mid outs
- if offsuit, 1x bet at least 3 high outs, or 2 high and 2 mid outs, or 5 mid outs
- fold all others
- 4th Street
- 1x bet small pair
- 3x bet 8 high suited outs
- 1x bet suited cards
- 1x bet 3 high and 1 mid outs
- 1x bet 2 high and 3 mid outs
- 1x bet 1 high and 5 mid outs
- 6 mid outs
- 5 mid outs, 1-gap
- 4 mid outs, 0-gap
- fold all others
- 5th Street
- 3x bet flush draw, or open-ended straight draw with all outs remaining
- 1x bet low pair, or straight draw
- 1x bet 5 high outs
- 1x bet 4 high and 2 mid outs
- 1x bet 3 high and 4 mid outs
- 1x bet 2 high and 6 mid outs
- 1x bet 1 high and 8 mid outs
- fold all others
How To Collude
You have to communicate with your fellow players at the start of the hand to learn your initial outs. For example, if you have K5o, you need to know how many Kings are out there. I’ve suggested a few ways for players to collude, and I think the simplest is for everyone to quietly announce their hand, in order. This only takes a few seconds, and everyone figures out their outs. For example, with K5o, all you need to know is if there are any Kings out there. If someone else holds a King, you fold. Otherwise, you 1x bet your hand. Then, as the dealer turns up the community cards, you know how many outs you pick up. Say 3rd Street is a 6. If no one 3x bets this card, this means you now have 3 high and 3 mid outs, enough to 1x bet and see 4th Street. On the other hand, if three people 3x bet this card, it means you only have 3 high outs, and you should fold your hand.
Notice the pattern of the minimum calling hands in the table. You can see that 2 mid outs are equal to 1 high out. This makes it easier to remember the cutoff points.
Easy Way To Play +EV Mississippi Stud
A lot of people love Mississippi Stud, but at a 5% house edge, the game is fairly expensive. On the other hand, if you can count your “outs” during the hand at a full table, you have a 1.5% player advantage over the house! That’s a 6.5% EV swing, and it’s a pretty simply matter to keep track of your outs. I’ll show you how to do this, without getting the floorman or the dealers upset with you.
First, you’ll need to play at a full table of 6 players. You only need to commute with the players at the start of the hand. On 4th and 5th Street, its very simple to track your outs, just by looking at the player bets (3x means they hit the board). So the key is finding out how many outs you have at the start of the hand. There’s a few ways to do this (all verbal).
The best way to share info is for each player to quietly announce their hand, in order. Each player says just what their hand is, e.g., “King Five” or “Ace Deuce” or “Six Trey”. This is a quick process, and takes a few seconds. No one asks anything, and there’s no talking over each other. Just listen, and each player knows exactly how many “outs” he has left.
This method requires cooperation, and can probably only work with friends. If you can’t get the players to follow this scheme, you still might be able to count your outs. You quietly announce your hand, look around (make eye contact with everyone) and hopefully they raise their fingers to tell you if they have your cards.
Ok, so lets say you know how many “outs” you have at the start of the hand. As you know from my collusion analyses, you know what the starting hands are (e.g., 5 mid outs, 3 high outs, 2 high and 2 mid outs, etc.). You make your 3rd Street bet accordingly.
The dealer then turns up 3rd Street on the board. You can tell by the 3x bets, how many “outs” remain for this card. For example, say 3rd Street is a Jack, and 2 people start betting 3x on the Jack. Almost certainly, that means there’s only one Jack left, so you can only add one high “out” to your hand. Or, let’s say that 3rd Street was an Ace, and nobody bets 3x on the card (and no one is screaming “three of a kind!”) Then, you can safely assume 3 more high outs for your hand.
It’s pretty simple to know if you should 1x bet to see 4th Street. You typically need 3 high outs, or 2 high outs and 4 mid outs, or 1 high out and 6 mid outs. See my decision charts for more details (e.g., low outs), but these are basically your thresholds.
The dealer then turns up 4th Street of the community cards, and again, it’s simple to see how many “outs” you’ve picked up. On 4th Street, low outs no longer matter. You typically need 5 high outs, or 4 high and 2 mid outs, or 3 high and 4 mid outs, or 2 high and 6 mid outs, or 1 high and 8 mid outs to 1x bet and see 5th Street. Again, see my decision charts for complete info, and details for raising draws.
That’s it. When you play the game with collusion, you should only be thinking about how many outs you have. Usually, I just care about high and mid outs. I don’t count my low outs, and just assume I have none. I don’t give up much EV with this tighter strategy. If you have a poker mind, this should be an easy way to play the game. Of course, you should practice on my flash game, which includes a 6 player collusion mode with your outs counted and displayed.
New Card Craps Practice Game
The best way to understand counting for card craps is to see it in action. I wrote a new practice game to demonstrate counting against the point, and when it’s correct to lay odds with your Don’t Pass bet. The game is configured with the Viejas parameters (10x odds, 312 cards in a ShuffleMaster 128 CSM) so if you’re planning to check out the game, practice here first! Sometimes I just like watching the rolls, so I also included an “Auto” mode to continuously play by itself. This might give you an idea of session variance, and what to expect if you actually decide to play 10x odds.
Click on the screenshot below to play:

I like watching all the animation and highlighting. It’s a lot more fun to run the game in a browser window, and occasionally see how it’s doing, than it is to sit and grind it out at Viejas all day 🙂
+EV Mississippi Stud: Why The House Doesn’t Worry
Lately, I’ve been playing more full exposure Mississippi Stud at my local Barona Casino. I’ve called it “the least enjoyable +EV game” around, because of it’s high variance. Generally, it’s an “expensive game”, played by an older crowd that can afford it. Even though the full exposure game is +EV (around +1.5% of the Ante) using a simple strategy, the game is only full (exploitable) on weekends. The way I think, people should be all over this game, keeping it full, betting $25 Antes, and grinding out $0.37/hand. But the game is usually empty for good reasons: it would take months of full-time grinding and a huge bankroll to take advantage of it. And you’d need a full team of 6 players.
Even when the game is full, the house’s hold (EV) is huge. Because there is no way on earth that people are going to play correctly, no matter what. I play with my cheat sheet, which tells me the approximate return of hands on 3rd and 4th street, and their exact returns on 5th street. Other players wouldn’t be caught dead following this advice, because it tells them to fold more than they like to (and occasionally, it tells them to raise more than they like to). Most players don’t like folding their hands, especially at 2nd street (first two cards), and at the river. They acknowledge that they shouldn’t “chase”, but they don’t know how bad (-EV) it is, and they get caught up in it.
The cheat sheet points out the cost of each mistake, and even the smallest mistake is usually in double digit territory. For example, if you’re on 2nd street, and you have only 1 high out and 2 mid outs, you’re giving up about a 31% house edge (of the Ante) to 1x call and see 3rd street. The return of this call is -1.31 Antes. Folding would be a better choice, costing only 1 Ante (-1.0 return). Calling will return -1.31 on average, or an additional 0.31 Ante loss to see a card. At a $5 Ante, this is an additional $1.55 cost over folding.
When you “chase” a hand, you often pick up just enough outs to “force” you to call again. In our 1/2/0 (high/mid/low outs) example, we called to see 3rd street, making our hand worth -1.31. If we pick up 2 more high outs on 3rd street, we now have a 3/2/0 hand, and we should 1x call again to see 4th street, since folding has a value of -2.0, while calling has a value of -1.75. Notice that we now have a hand that is 0.75 Antes worse than folding on 2nd street (-1.0 Antes), and we’re forced into investing 3 Antes. Chasing could get worse. If we pick up another 2 mid outs on 4th street, we’re again forced into another 1x call, to “protect” our 3/4/0 hand and 3 Ante investment to extract out its -2.94 Ante value (would be -3.0 to fold on 5th street). So that’s how a 31% mistake escalates to a -300% cost. Of course, if we paired up our hand, we could win big. That’s why it’s only a 31% mistake on average.
“Chasing” is horrible, because you should just fold and wait for the next hand, instead of forking out -EV to the house. If you don’t hit, EV just gets worse. Often at the table I hear, “I always see the first card”, meaning they’ll play any two cards to 3rd street. I simulated this “call anything” 3rd street strategy combined with perfect strategy on 4th and 5th street, and the result was a 13.5% house edge. Notice that’s worse than having no other information and playing basic strategy (4.91% house edge). It’s no wonder that most people lose a tremendous amount of money at the game. It’s hard to say, but I’d guess the average player is giving up about a 20% (of an Ante) edge to the house. At a $5 Ante, that’s $1 a hand.
Of course, that $1/hand cost might be the marginal utility of “not folding” + “getting lucky” + “playing hunches” – “bleeding off” to that player. I’m kind of the exception. To me, giving up a 5% edge to the house on a mistaken call feels a lot worse than its $0.25 average cost 🙂





leave a comment